• Math tutors
• /
• Knowledge Base
• /
• 90 Degree Angle – Measurement, Definition With Examples

90 Degree Angle – Measurement, Definition With Examples

Phoebe Belza-Barrientos

reviewed by Janice S. Armas

Updated on October 30, 2025

Ready to become a master of geometry? You’re in the right place, with another informative and educational article from Brighterly!

Today, we’re going to explore the 90 degree angle – a common angle in geometry also known as a right angle. This angle forms part of many shapes, and we can see it in our everyday lives too. Think about the corner of a table, a book, or even a street corner. They are all 90 degree angles!

Here, you’ll learn how much is 90 degrees in an angle, the properties of this angle, and how it’s different from other angles. We’ll also provide some practice questions for you to try out.

What is a 90 degree angle?

A 90 degree angle is an angle that measures exactly 90 degrees. You might also know it as a right angle, and you’ve probably already come across it in math via squares, rectangles, and right-angled triangles. Also, please notice that a 90 degree angle makes a corner shape, and it is formed when two lines intersect perpendicularly. Some people wonder if there is a 90 degree angle formula, but there isn’t one.

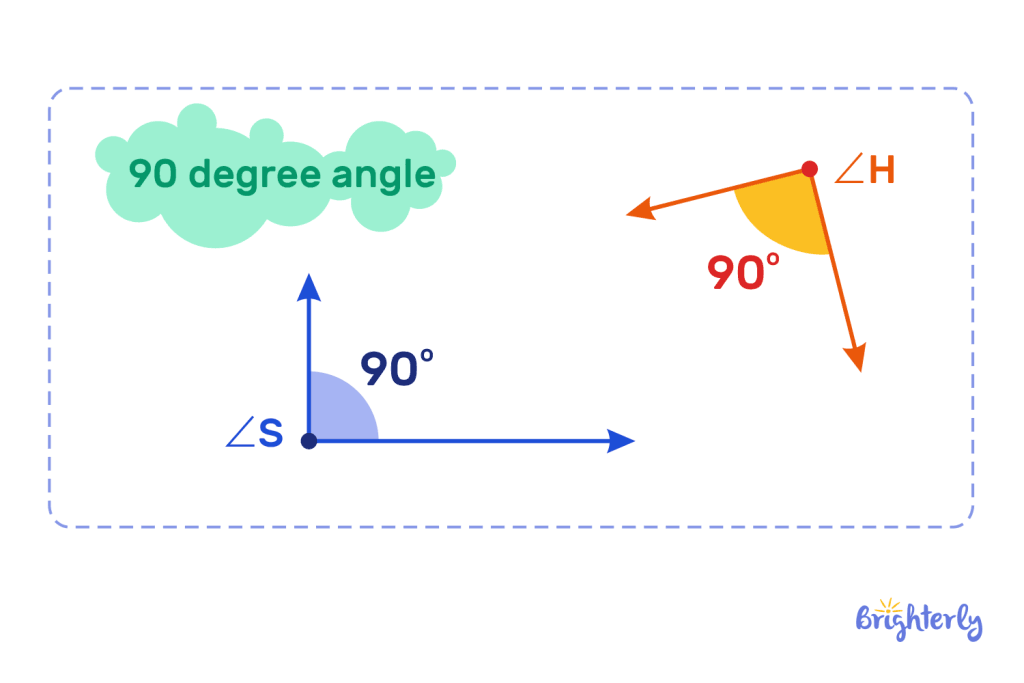
Definition of a 90 degree angle

So, what is a 90 degrees angle? The definition of a 90 degree angle states that it’s an angle that features two perpendicular lines that intersect to form exactly 90 degrees in measurement. You’ll notice that, as well as forming a corner, it forms an L shape, which is why it can be represented by the ∟ symbol.

Properties of a 90 degree angle

Now that you know what is 90 degrees, it’s time to explore the properties of this angle. The properties of a 90 degree angle are:

• Two lines that intersect perpendicularly create an angle. You’ll also know it as a right angle.
• Features in many shapes as standard, like squares, rectangles, and right-angled triangles
• If two angles form to create a 90° angle, they are called complementary angles. 
• It is half the size of a 180 degree angle, which is a straight line.

Measurement of a 90 degree angle

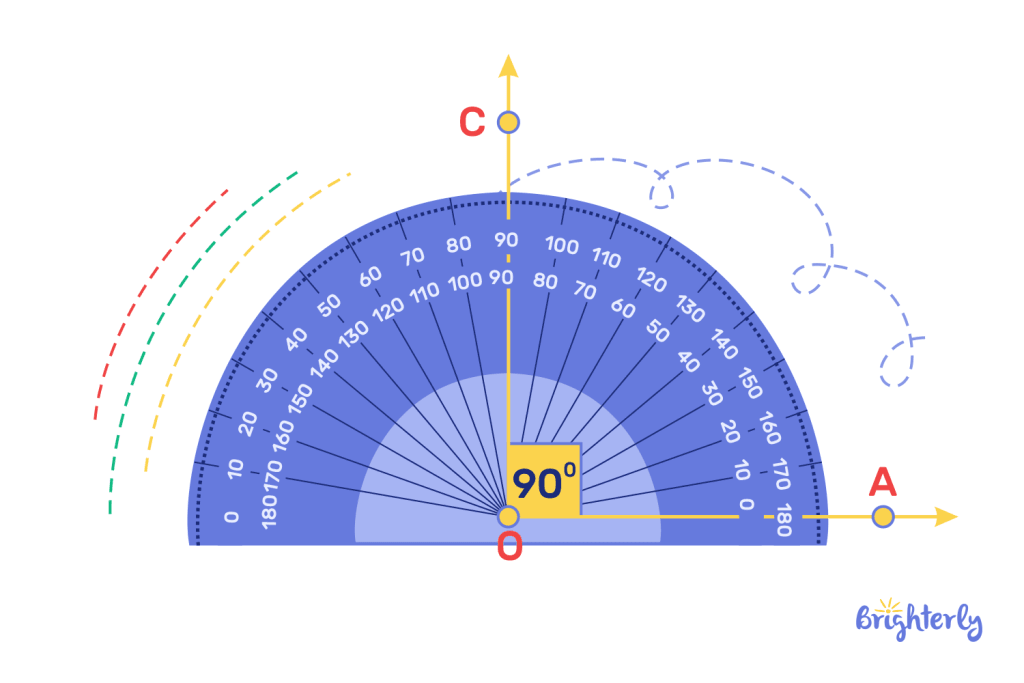
If you’re looking to measure a 90° angle, you’ll get the best results using a tool called a protractor. This semicircle-shaped tool measures angles up to 180 degrees wide. 

To use the protractor, simply align the protractor’s base (the straight edge) with one of your lines, then note which number the other line hits. This is the degree of your angle. In the case of the 90 degree angle, it will exactly match the middle of the protractor.

90 degree angle in geometry

The 90 degree angle is commonly found in geometry. It forms many common shapes we recognize, including rectangles and squares. It can also be found in some other polygons and one specific type of triangle – the right-angled triangle. If you use a graph, the horizontal and vertical axes of the graph will form a 90 degree angle. It also relates to the Pythagorean theorem.

Math tutors

Join Brighterly for personalized lessons for your child.

Meet the best tutors for interactive math learning.

Let’s start learning Math!

Difference between 90 degree angle and other angles

Primarily, the difference between the 90° angle and other angles is that they have different measurements. But there’s more to it than that. All angles that are: 

• smaller than 90 degrees are called acute angles
• larger than the right angle but smaller than a 180 degree angle are called obtuse angles. 

The 180 degree angle is known as a straight angle, and any angles larger than this are known as reflex angles.

Examples of 90 degree angle in everyday life

Looking for a 90 degrees angle example in everyday life? There are many! These include:

• The corners of a book
• The corners of a table
• The corners of your house
• The corners of TVs and computers
• Street intersections

Creating a 90 degree angle: Step-by-step procedure

To create a 90 degrees angle, it’s easiest to use a tool called a compass. Here’s a step-by-step guide to drawing a 90 degree angle:

1. Draw a straight line
2. Place your compass point on one end of your line and draw an arc above your line
3. Place your compass point on the other end and repeat, making sure the arcs intersect
4. Draw a straight line from the intersection to your original line

Drawing a 90 degree angle using a protractor

You can also draw a 90 degree angle using a protractor. Here’s how to do it, step by step:

1. Draw a straight line
2. Place your protractor base on your straight line, identify 90 degrees on your protractor, and mark it
3. Remove your protractor, and draw a straight line connecting to your original line

Practice problems on 90 degree angle

Are you ready to try out some problems on 90 degree angles for yourself? Our practice problems below are designed to test your new knowledge – simply grab a pen and paper and answer the questions!

1. Draw a 90° angle on a piece of paper using only a protractor.
2. Identify some objects in your home that have a 90-degree angle and write them down.
3. If you have an angle that is twice the size of a right angle, what is the size of this angle in degrees?

Conclusion

Now you have a clear answer to the question of “What is a 90° angle?” and also responses to other queries. Besides, you know that this angle has many interesting properties and can be seen in many mathematical and everyday objects. You’ve just taken a big step in your journey of mastering geometry!

Frequently asked questions on 90 degree angle

What is a 90 degree angle?

A 90 degree angle is an angle that measures exactly 90 degrees. It is also known as a right angle, and is formed by two perpendicular lines intersecting. The 90 degree angle can be seen in many geometrical shapes, from squares and rectangles to the axes of a graph.

What does a 90 degree angle look like?

A 90 degree angle looks like a corner, or an L shape. You could also say that it looks like everyday objects like corners of paper, books, or tables.

How to draw a 90 degree angle?

You can draw a 90 degree angle using a protractor by first drawing a straight line. Then, line up the base of your protractor with the line, identify the 90 degree point, and mark it. Then, draw a line that connects to your first line.

Where do we see 90 degree angles in everyday life?

You’ll see 90 degree angles in lots of objects and places. 90 degree angle example includes the corners of magazines, tables, TVs, and tablets. You’ll also see them in the form of street corners and intersections. 90 degree angles are everywhere!

Phoebe Belza-Barrientos

13 articles

Phoebe Belza-Barrientos is a Brighterly math tutor with 13 years of teaching background. Math is far more than just another basic subject for Phoebe; it’s a passion she now channels into every lesson. She builds study materials in a way that her students begin to feel the same discovery and enjoyment as she did in her school years.