• Math tutors
• /
• Knowledge Base
• /
• Adjacent Angles – Definition With Examples

Adjacent Angles – Definition With Examples

Jo-ann Caballes

Updated on January 6, 2026

Adjacent angles aren’t as difficult as they may seem at first glance. At Brighterly, we strive to explain all geometry ambiguities in simple terms. And today, all ambiguities with adjacent angles will become understandable. So, let’s explore whats an adjacent angle is through the definition, examples, and practice problems.

What are adjacent angles?

Adjacent angles are the angles that share a common vertex and a common side, but do not overlap. They are angles that are side by side, touching at a single point, and not intersecting or overlapping. This is how adjacent definition geometry is explained.

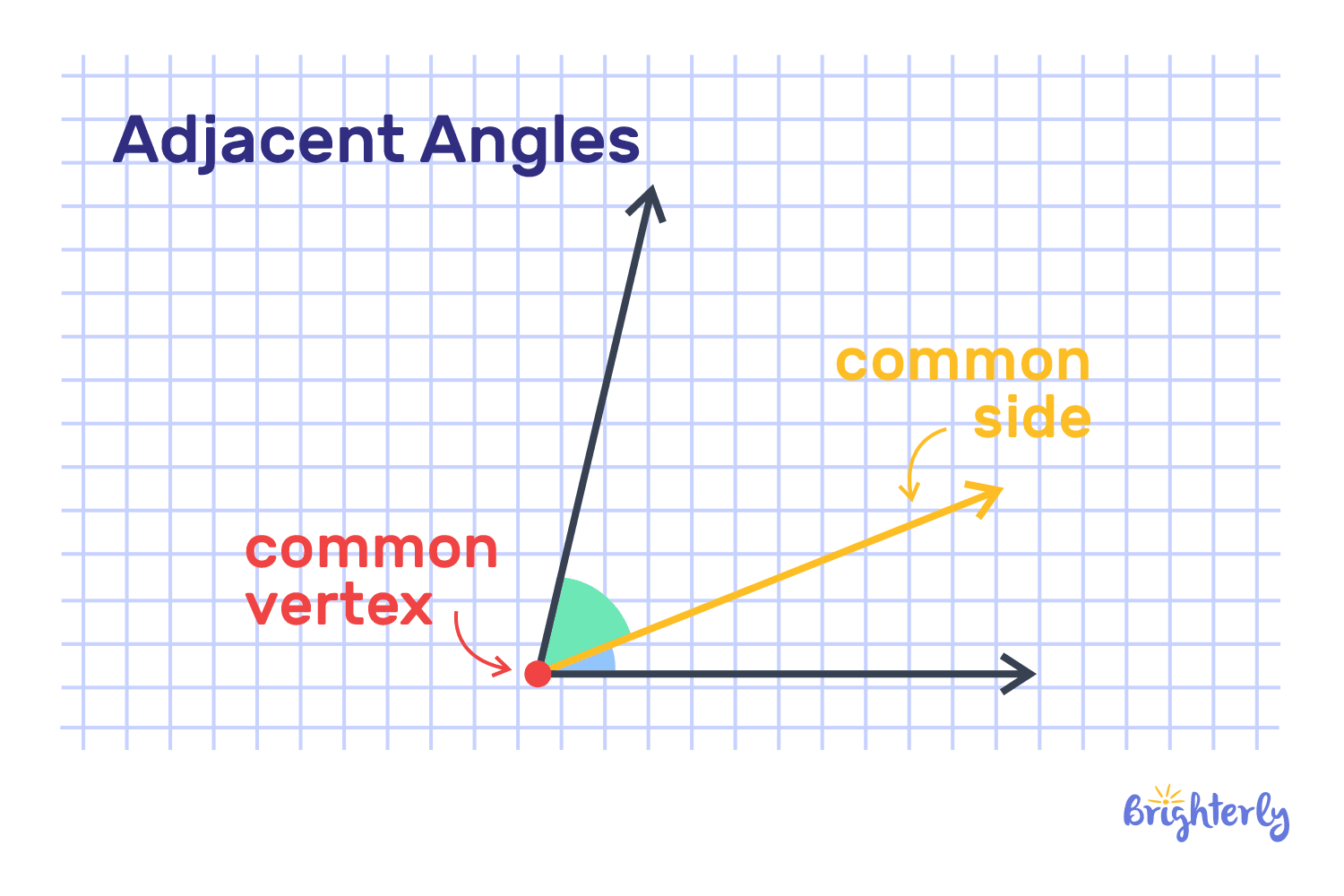
Typically, a shared side is a ray, and a shared vertex is its endpoint. When two adjacent angles form a straight line, they create a straight angle (a linear pair).

Definition of adjacent angles

Angles with a common vertex and side are known as adjacent angles. There is no overlap between them, and they are directly next to each other. This is the adjacent definition that math proposes.

Adjacent angles examples

After we explored the adjacent angle definition, let’s go through some examples of them:

• Consider a door with hinges on its edge. The angle formed by the door and the frame at each hinge is called an adjacent angle. There is a share­d vertex (the hinge) and a share­d side (the edge of the door) between these adjacent angles.
• At a road intersection, some angles next to each other share a common side and vertex, so they are adjacent. 

Math tutors

Join Brighterly for personalized lessons for your child

Meet the best tutors for interactive math learning.

Book free lesson

Adjacent angles: Properties

Adjacent angles definition geometry explains that the adjacent angles have the following properties:

• A common vertex is the most important property of adjacent angles. When two rays intersect, they form a common endpoint.
• There is also a common side between adjacent angles. It means that each angle has one side that is the same, and some adjacent angles form a straight line. In this case, they are called a linear pair.
• Adjacent angles don’t overlap; they are always next to each other. Their interiors are completely different.

How to find adjacent angles?

There are two main properties that help identify adjacent angles – they always share a common side and a common vertex. An angle will not be considered adjacent if it satisfies just one of these properties. In order for angles to satisfy both properties, they must meet both criteria. For example, if two angles share a vertex but have an angle in between, they do not share a side. Therefore, they cannot be adjacent angles. 

The following figure shows adjacent angle meaning.

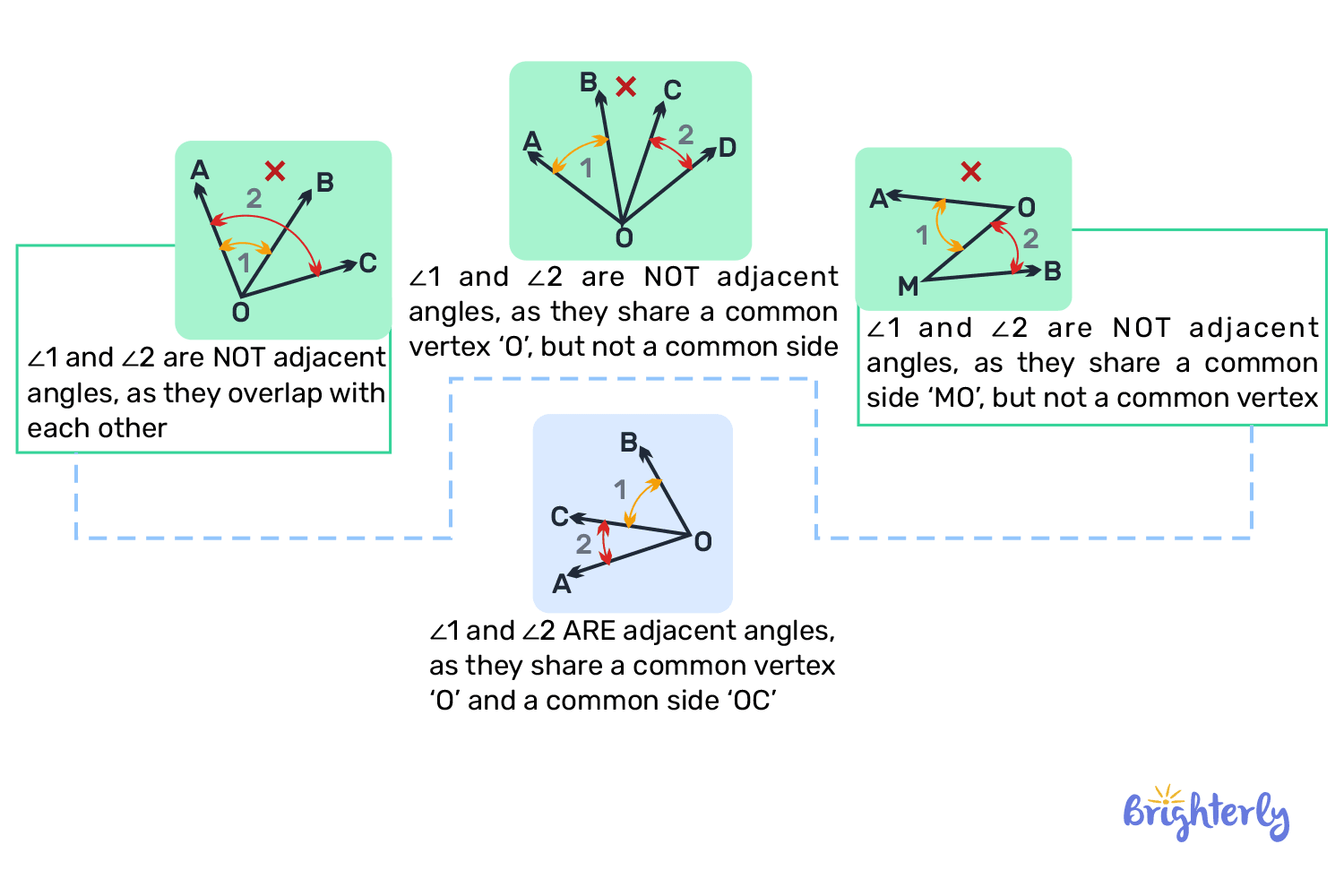
Here are some important notes about adjacent meaning in math:

• If two angles are adjacent, then their sum is the angle formed by two non-common arms and one common arm.
• Whenever rays form a straight line, their angles add up to 180°.
• Adjacent angles meaning keep the fact that an angle pair that has a sum of 180° is referred to as a linear angle pair. The sum of supplementary angles in all linear pairs is 180°, so they are all supplementary. However, not every supplementary angle must be a linear pair. There must be an intersection of lines and an angle formed between them in order for a linear pair to be formed.
• When two adjacent angles sum to 180°, they form a straight angle.

Adjacent angles real life examples

1. Clock hands. The angles formed by the hour hand and minute hand at any given time can create adjacent angles. Example: At 3:00, the hour hand and minute hand form two angles next to each other sharing a vertex (the center of the clock) and a common side.
2. Book pages. When a book is partially opened, the angles formed by two consecutive pages next to each other are adjacent. They share a common edge (the spine) and a vertex (the fold of the book).
3. Door hinges. The angles formed by a door and its frame when the door is partially open. The angle between the door and the frame is adjacent to the right angle of the hinge.
4. Intersecting roads or paths. The angles formed at street intersections where two roads meet form adjacent angles. They share a common vertex (intersection point) and a common side (the road line).
5. Walls in a room. Corners of a room create adjacent angles. Each angle shares a common side (wall) and a vertex (corner).

Adjacent angles worksheets

At Brighterly, we believe that practice leads to mastery. You can find a variety of additional practice questions with answers on our angles worksheets:

• Types Of Angles Worksheets
• Missing Angles in Triangles Worksheets
• Pairs Of Angles Worksheets
• Coterminal Angles Worksheet

Solved examples on adjacent angle

Let’s see an adjacent angle example in different problems below.

Example 1: Two adjacent angles are supplementary. If one angle measures 110°, find the measure of the other angle.

Solution: Supplementary angles add up to 180°. If one angle is 110°, the other angle is:

180°−110°=70°

Answer: 

Example 2: Two adjacent angles form a straight line. One of the angles measures 125°. Find the measure of the other angle.

Solution: Angles on a straight line are supplementary, so their sum is 180°.

180°−125°=55°

Answer: 

Example 3: Two adjacent angles are complementary. If one angle is twice the other, find their measures.

Solution: Let the smaller angle be x. Then the other angle is 2x. Since they are complementary:

x+2x=90°

3x=90°3

x=30°

The other angle is:

2x=60°

Answer:

Example 4: Two adjacent angles form a right angle. One angle is 25° more than the other. Find both angles.

Solution:  Let the smaller angle be x. Then the larger angle is x+25°. Since they are complementary (sum = 90°):

x+(x+25°)=90°

2x+25°=90°2

 2x=65°

x=32.5°

The other angle is:

32.5°+25°=57.5°

Answer:

Adjacent angles: Practice problems

1. Two adjacent angles are supplementary. If one angle measures 75°, what is the measure of the other angle?
2. In a rectangle, one of the adjacent angles measures 90°. Find the measure of the other adjacent angle.
3. Two adjacent angles form a right angle. If one angle is 35°, find the measure of the other angle.
4. Two adjacent angles are complementary, and one angle is twice the other. What is adjacent angles? Find them both.

Frequently Asked Questions on adjacent Angles

What is an adjacent angle?

Adjacent angles are two angles that share a common vertex and a common side, and lie next to each other without overlapping. They appear side by side in the same plane. This is the common adjacent angles definition.

Which angles are adjacent angles?

Angles that have a shared vertex and a common side, and do not overlap, are adjacent. They can be part of geometric shapes, intersecting lines, or real-life structures like doors, clocks, and book pages.

How to find adjacent angles?

To find adjacent angles, identify angles that share a vertex and a side. If their measures are known, you can use addition or subtraction rules, depending on whether they are complementary or supplementary.

Are complementary angles always adjacent?

No, complementary angles are not always adjacent. They sum to 90°, but they may be separate and not share a common side or vertex. Only some complementary angles are adjacent.

Jo-ann Caballes

18 articles

As a seasoned educator with a Bachelor’s in Secondary Education and over three years of experience, I specialize in making mathematics accessible to students of all backgrounds through Brighterly. My expertise extends beyond teaching; I blog about innovative educational strategies and have a keen interest in child psychology and curriculum development. My approach is shaped by a belief in practical, real-life application of math, making learning both impactful and enjoyable.