Altitude of a Triangle – Formulas, Definition With Examples
reviewed by Camille Ira B. Mendoza
Updated on October 28, 2025
Brighterly has prepared just the right material to help you explore triangle altitude in definition geometry and learn more about its properties.
Triangles have many unique features, properties, and tools that help us understand them better. Today, we’re going to explore the altitude of a triangle. The altitude is one of many features of this unique shape and can help us work out other properties of triangles, such as their area or diameter, if we don’t have information like their side lengths.
Here, we’re going to explore the definition of triangle altitudes, properties of triangles, and how to find altitude of a triangle. You’ll also get the chance to analyze some practice math problems to put your skills to the test.
What is an altitude of a triangle?
The altitude of a triangle is a line that stretches down from one of its vertices (corners) to the base (the bottom of the triangle). Once you take a look at a vertex, you’ll find that it forms a right angle of 90° with the now perpendicular line of the base.
But we don’t just identify and draw the altitude of a triangle for fun – this simple geometrical concept can help us identify many other properties of our triangle, from its area to more complex mathematical problems. This is especially useful if we’re missing information like its side lengths.
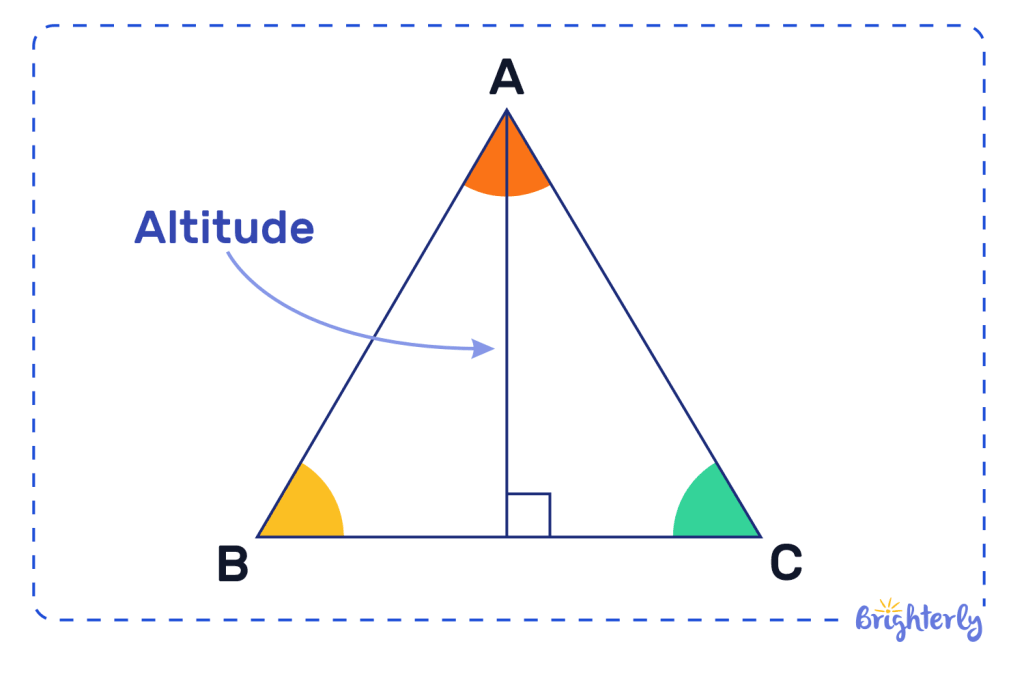
Definition of a triangle
The definition of a triangle is a 2D geometric shape with 3 sides. All 3 sides of this shape are straight lines, which create 3 vertices and 3 internal angles. All of the angles within a triangle add up to 180°. There are lots of different types of triangles, including:
- right-angled triangles
- scalene triangles
- obtuse triangles
- isosceles triangles
- equilateral triangles.
Definition of altitude in a triangle
The definition of altitude in a triangle is a straight, vertical line that stretches down from one of the triangle’s vertices to its base, which is usually its opposite side. It can also be referred to as the height of a triangle.
In an obtuse triangle, the altitude will be drawn outside of the triangle to form the right angle rather than the inside, because the angle opposite to the vertex is obtuse.
An altitude of a triangle real life example is measuring the area of a triangle-shaped building – this can help architects understand the space available inside the structure. Exploring real-life examples of these concepts helps you understand their place in the world.
Properties of triangles and their altitudes
There are lots of properties of both the geometric shape of the triangle and its altitudes. Many properties apply to all triangles, and then each individual type of triangle has its own set of properties that make it distinctive.
Properties of triangles
There are many different types of triangles, but they will always share these common properties:
- Triangles will always have 3 straight sides, 3 vertices, and 3 internal angles
- The internal angles in triangles will always add up to 180°
- The longest side of your triangle will always be directly opposite the biggest angle
- The shortest side of your triangle will always be directly opposite the smallest angle
These properties are true of equilateral, isosceles, scalene, and right-angled triangles, which then all have additional properties in their own right.
Properties of altitudes in triangles
Altitudes in triangles also have their own distinctive properties. These are:
- The altitude is a straight line that forms a right angle with the base of your triangle
- The triangle altitude intersects the base of your triangle
- It creates a line of symmetry in equilateral triangles, bisecting the shape into 2 halves
- The altitude represents the shortest distance between your triangle’s base and the vertex
Difference between a triangle and its altitude
The difference between a triangle and its altitude lies in the fact that the triangle is a geometric shape, and the altitude is an element of that shape.
The altitude helps us determine certain facts about the triangle, like its area. This is a key use when we don’t know other dimensions of the triangle, like its side lengths. It can also be used to understand shapes in or around the triangle, making it a multi-purpose tool.
If we look at an altitudes of triangles real life example, measuring the area of a mountain is a good one. The altitude is the height of the mountain, while the triangle is its shape.
Formulas involving the altitudes of triangles
The most important altitude of triangle formula is the one you’ll use the most:
Area = ½ base x altitude.
This formula helps you calculate the area of a triangle using the altitude.
Deriving the formula for the altitude of a triangle
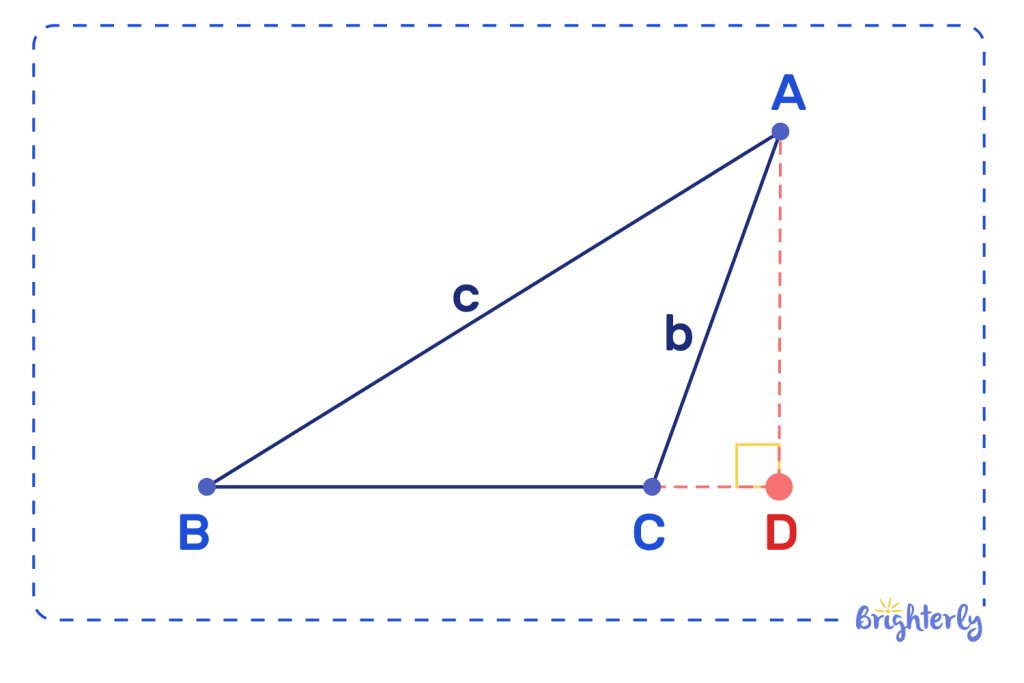
Like many triangle formulas, the altitude of a triangle formula can be derived from the Pythagorean theorem. This key geometric theorem tells us that the square of the length of your hypotenuse in a right-angled triangle (the side across from the right angle) is the same length as the sum of the other two sides, squared.
Writing formulas involving altitude in triangles
Writing formulas involving altitude in triangles might seem complicated, but it’s actually pretty straightforward once you know how! If we take the example of a right-angled triangle with ABC as its angles, BC as its base, and AB as its altitude, we can use the Pythagorean theorem to write the formula.
This formula would be AB = sqrt(AC2 – BC2) – in this formula, AC is the hypotenuse and BC is the base of your triangle.
Practice problems on the altitude of a triangle
Now that we’ve equipped you with all the essential knowledge, it’s time to put it into practice. Try out these test questions to see if you’ve grasped this information.
Problem 1: Find the area of a triangle with a base of 10 units and an altitude of 5 units
The formula for the area of a triangle is 1/2 * base * altitude. If we substitute the given values, we have Area = 1/2 * 10 units * 5 units = 25 square units. So, the area of a triangle with a base of 10 units and an altitude of 5 units is 25 square units.
Problem 2: A triangle has a base of 15 units and an area of 45 square units. What is its altitude?
If we know the area of a triangle and its base, we can rearrange the area formula to find the altitude. Altitude = (2 * Area) / base. Substitute the given values, and we have Altitude = (2 * 45 square units) / 15 units = 6 units. So, the altitude of the triangle is 6 units.
Conclusion
From this knowledge base, you now know what the altitude of a triangle is, its properties, what it’s used for, and its formulas. This essential knowledge is key to helping you become a geometry whizz and provides foundational information that will be useful as you tackle more complex concepts.
Frequently asked questions on the altitude of a triangle
What is an altitude in geometry?
The altitude meaning in geometry is a line that stretches from the vertex of a shape to its base. Usually, the shape is a triangle, and the altitude helps us to work out its properties like area. However, overall, the altitude geometry is the height of a shape.
What is the altitude of a triangle?
The altitude of a triangle is a straight line segment that stretches from the vertex (corner) of a triangle to its base (bottom). It’s an essential geometrical concept that helps us work out the areas of triangles and has unique properties.
What is the difference between a triangle and its altitude?
The difference between a triangle and its altitude is that a triangle is a shape, and the altitude is a line segment used to work out properties of that shape. Both are integral to geometry, but their differences lie in their types and applications.
How to find the altitude of a triangle?
To find the altitudes of a triangle, simply identify the base of your triangle and the vertex opposite its base. Next, connect the two by drawing a straight line segment. There you have it, you’ve successfully found the altitude triangle!
How is the altitude of a triangle used in real life?
There are many uses for the altitude of a triangle in real life, including measuring mountains and buildings, understanding structural stability in construction projects, and measuring the elevation of land. Measuring the heights of the pyramids in Egypt is a real life example of altitude of a triangle.






