Arithmetic – Definition with Examples
reviewed by Jo-ann Caballes
Updated on December 21, 2024
Welcome to Brighterly, where we make math interesting to learn and easy to understand!
Today, we’re covering arithmetic.
We’ll discover the arithmetic meaning, arithmetic math examples, basic rules of arithmetic and frequently asked questions. We’ll also share math worksheets and practice test questions so you can continue your learning!
What is arithmetic?
Arithmetic math is a fundamental branch of mathematics. It includes four key math operations, the equal sign and inverse operations. We cover the arithmetic definition and examples below.
Arithmetic definition
The definition of arithmetic is the branch of mathematics that covers four basic operations (addition, subtraction, multiplication and division), the equal sign and inverse operations. It forms the foundation of more complex math concepts.

Basic rules of arithmetic
There are some rules that form the basis of basic arithmetic:
- Addition and subtraction
- Multiplication and division
- Equal sign (“=”)
- Inverse operations
Let’s study the arithmetic operations examples below.
Addition and subtraction
Addition and subtraction are the two first math operations you’ll master.
Addition
Addition means adding two arithmetic numbers together to make a total (aka a sum). Your numbers are your addends and your final number is your sum. In equation 5 + 6 = 11, 5 and 6 are addends and 11 is the sum.
Subtraction
Subtraction means removing one number from another. In a subtraction equation, you have minuends, subtrahends and the difference. In equation 9 – 6 = 3, 9 is the minuend, 6 is the subtrahend and 3 is the difference.
Multiplication and division
Multiplication and division are the two other simple arithmetic operations. You’ll be introduced to them after addition and subtraction.
Multiplication
Multiplication is multiplying one number by another – an easy way to think about it is repeated addition. In the equation 2 x 4 = 8, you’re adding 2 together 4 times – 2 + 2 + 2 + 2 = 8. Is arithmetic multiplication? No, but multiplication forms a part of arithmetic.
Division
Division is opposite to multiplication. To divide, you split a number into equal parts – for example, in the equation 14 ÷ 7 = 2, you’re dividing 14 into 7 equal parts of 2. Here, 14 is a dividend, 7 is the divisor and 2 is the quotient.
Equal sign (“=”)
The equal sign (=) indicates that two sides of an equation are equal to one another, i.e. they represent the same value. An example of arithmetic equal sign is in the equation 8 + 12 = 20, 8 + 12 is equal to 20.

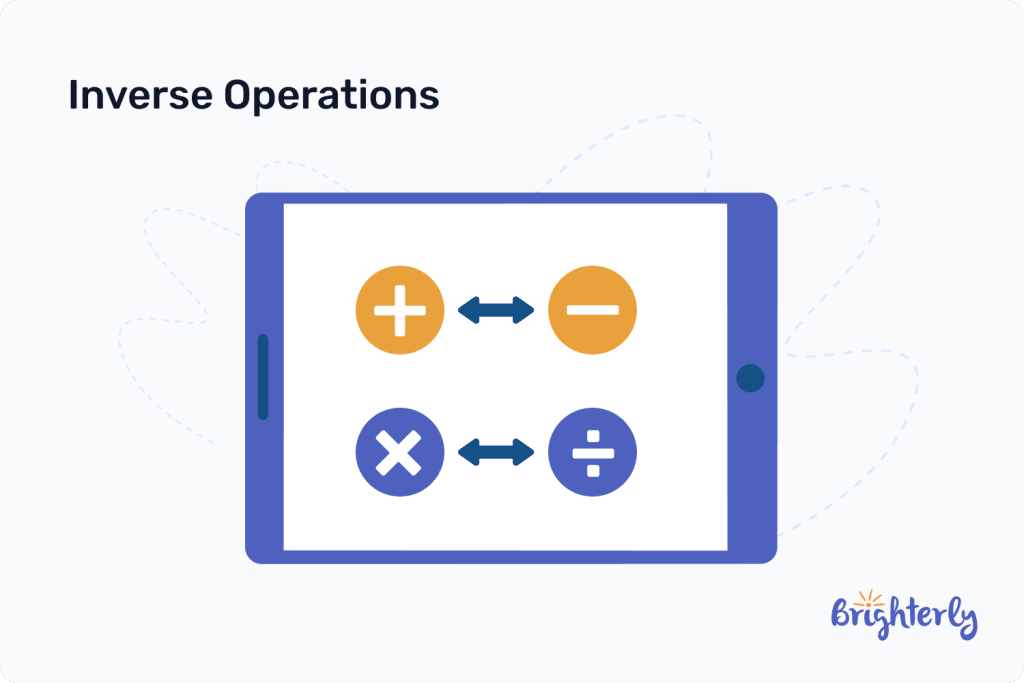
Inverse operations
Inverse operations are the ones that perform the opposite function and therefore cancel each other out. For example, 5 + 9 = 14, and the inverse operation of subtraction means 14 – 9 = 5 cancels the addition out.
Solved examples on arithmetic
Ready to put your newfound knowledge of arithmetic meaning in math to the test? Try out our solved math problems and check your answer to see how many you get right!
Solved math task 1
Solve the equation: 15 + 12.
Answer:
| 27. |
Solved math task 2
Solve the equation: 4 x 9.
Answer:
| 36. |
Basic arithmetic: practice math problems
Frequently asked questions on arithmetic
Why do we need to learn arithmetic?
We need to learn arithmetic because it’s the foundation upon which all math is based. In order to understand more complex math problems, like algebra and geometry, we first need to understand arithmetic. So if you’re wondering, “What is arithmetic in algebra?”, it forms the basis of algebra. It’s also essential in daily life, from counting money to measuring baking ingredients.
Are there more operations in arithmetic besides the basic ones?
Yes, there are more operations in arithmetic besides the basic ones. These include roots, logarithms and exponentiations. You’ll learn about these operations once you’ve mastered the arithmetic basics.
What is the order of operations?
The order of operations tells us which order to carry out operations in when we have a complex equation. It goes: parentheses, exponents, multiplication and division (left to right), addition and subtraction (left to right). It can be remembered with the acronym PEMDAS.
What are inverse operations in arithmetic?
The inverse operations in arithmetic are addition and subtraction and multiplication and division. They are inverse because when performed, they cancel each other out.
Why is the equal sign important in arithmetic?
The equal sign is important in arithmetic because it completes an equation. It shows the result of an operation and indicates that one side of an equation is equal to the other.
Arithmetic worksheets
Put your knowledge to the test with our engaging arithmetic worksheets!
- Addition and subtraction worksheets
- Multiplication worksheets
- Missing addend worksheets
- Adding and subtracting integers worksheets