Completing the Square – Definition with Examples
Updated on February 8, 2026
Hello and welcome to another Brighterly knowledge base article, where we will be looking into and simplifying another math topic. In today’s menu is a powerful algebraic technique called completing the square.
While the name suggests it may be a geometry topic, completing a square is actually all about algebra and is a clever way to rewrite quadratic equations to make them much easier to solve. In this article, we will lookinto how to complete a square, what the definition of completing the square is, and what the purpose of it is. Let’s start!
What is completing the square?
In algebra, when we need to complete the square, we need to transform a quadratic expression from its standard form, ax^2 + bx + c, into what in math is called a “perfect square trinomial.” A perfect square trinomial is the expression that you can write as the square of a simple binomial, like (x + d)^2.
Knowing how to do this is not only an essential math skill, but a useful one too, as it can help your child to easily factor the equations by hand, as they now look much simpler.
Complete the square definition
Completing the square definition in math, in its simplest form, would be the process of taking a quadratic expression and rewriting it to get a perfect square trinomial plus or minus a constant. When you do this completion process correctly, the equation you have should be transformed from the standard form ax^2 + bx + c into the vertex form a(x – h)^2 + k.
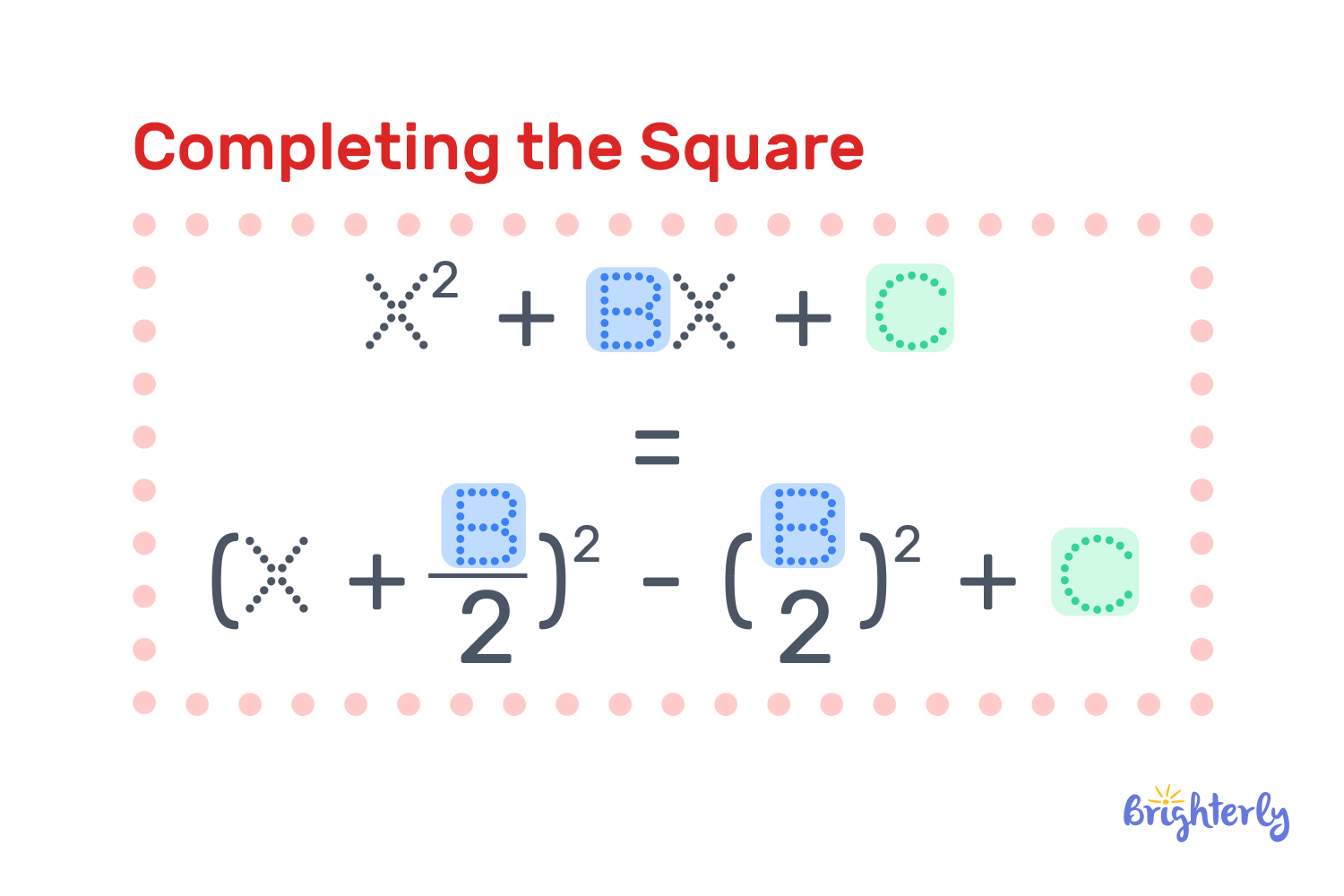
Explanation of the completing the square process
Let’s look at completing the square steps. To do this, you need to focus on the x^2 and x terms.
At the first step, you need to make sure that the coefficient of x^2 is one. If it isn’t, you need to divide your equation by its coefficient. Next up, you need to move the constant to the other side of the equation, to only have x^2 and x left. Then, you need to take the middle coefficient (let’s call it b), halve it, and then square it. You then add that number to both parts of the equation. And then the last step comes, where you need to write your equation as a perfect square trinomial.
Purpose of completing the square
When students learn how to complete square, one of the questions they have is what is the purpose of it all. Why learn this specific technique at all? After all, it takes a lot of steps.
The answer is, it’s a “Swiss army knife” type of skill in algebra, and as your child dives deeper into it, this technique will come in handy. They will encounter most of the completing the square practice problems when solving non-factorable equations, finding the vertex form, graphing circles, and as they dive deeper into the quadratic formula (the sometimes scary-looking ax^2 + bx + c = 0 format). By knowing this technique, your child will be able to transform complex-looking formulas into simpler and more manageable ones and solve them more easily.
Completing the square method
One important feature of how to complete square method is how balanced and systematic it is. In Algebra, maintaining the balance is critical: you can’t just add a number to an equation because you want to or because it would make the process easier. You need to keep both sides equal.
The process behind completing the cycle technique is that it gives you that balance, although through a series of steps, so that you fold one type of equation into another type, while maintaining its architecture and value. The logic, and the whole point of the process, is to figure out the missing number that makes the puzzle complete.
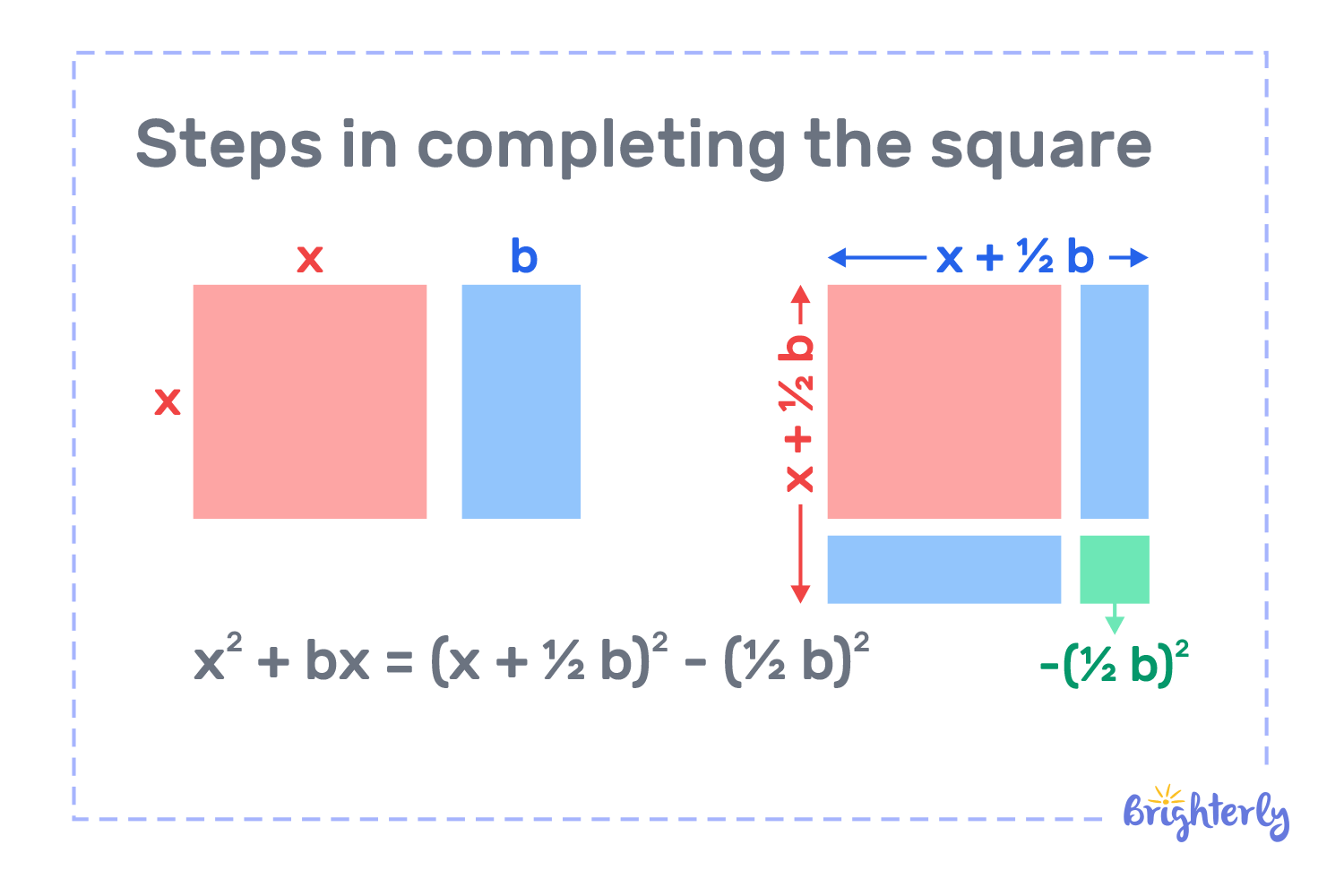
Steps in completing the square
We’ve looked at the steps on how you can complete the square steps correctly earlier in the article. Now, let’s look at how completing the square example will look in the case of x^2 + 4x + 2 = 0
- x^2 + 4x = – 2
- b = (4 ÷ 2)^2 = 2^2 = 4 (in this case, we ended up with the original number, but it’s not always the case)
- x^2 + 4x + 4 = 2
- x^2 + 4x + 4 = (x + 2)^2 = 2
After you correctly follow these steps to completing the square, you’ll have a perfect square trinomial.
Formula for completing the square
As with almost everything else in math, completing the square technique has its formula. At first sight, the formula might seem a bit scary, but the process behind it is quite simple, as you’ve seen earlier.
If you have the quadratic form x^2 + bx, you need to find the formula that will complete it. That formula is (b/2)^2. You add it to your quadratic form, and the answer will be your perfect square trinomial, like so:
x^2 + bx + (b/2)^2 = (x + b/2)^2
And there you have your formula. You can think of it as a completing the square calculator, where you just plug in your letters and values, and get your perfect square trinomial on the other side.
Completing the square examples
Let’s now look at a couple of complete the square examples to give you a better idea of how to approach the process.
Example 1 is the equation x^2 + 6x – 7 = 0
First, we move the constant: x^2 + 6x = 7
Then, apply the formula to the middle coefficient: (6 ÷ 2)^2 = 3^2 = 9
Add the 9 to both sides: x^2 + 6x + 9= 7 + 9
Factor into a square: (x+3)^2 = 16
Solution: We get x + 3 = ±4, so x = 1 or x = -7
Example 2 is the equation x^2 + 4x + 1 = 0. Here is how you will solve the equation by completing the square:
x^2 + 4x = -1
b = (4÷ 2)^2 = 2^2 = 4
x^2 + 4x + 4= -1 + 4
x^2 + 4x + 4 = 3
(x+2)^2 = 3
x + 2 = ±√3
Quite easy, isn’t it? Your kid will get the grasp of it with just a few problems!
Completing the square worksheet PDF
To strengthen what your kid learned in class and in this article, they need to practice. By solving problems and going through each step several times, they will develop a deeper understanding and a sort of muscle memory that won’t fade away soon. They can get that practice with free Brighterly Completing The Square Worksheets, which come filled with a wide range of completing the square examples and exercises.
Solving tasks on completing the square
Solved task 1
Let’s solve the equation x^2 – 8x + 12 = 0 for x.
Solution: We start by moving the constant to the right side and finding the “magic number” b:
- x^2 – 8x = -12
- b = (8 ÷ 2)^2 = 4^2 = 16
We then add the number b to both sides of the equation, take the square root, and solve for x
- x^2 – 8x + 16 = -12 + 16
- x^2 – 8x + 16 = 4
- (x – 4)^2 = 4
- x – 4 = ±2
|
x – 4 = ±2 → x = 4 ± 2 → x = 6 and x = 2 |
Solved task 2
Solving x^2 + 3x – 1 = 0 for x
Solution: The solution follows the same steps as the earlier.
x^2 + 3x = 1
b = (3/2)^2 = 9/4
x^2 + 3x + 9/4 = 1 + 9/4
(x + 3/2)^2 = 13/4
| (x + 3/2) = ± √13 / 2 |
Solved task 3
Let’s solve for x by completing the square: x^2 – 10x + 21 = 0
x^2 – 10x = – 21
b = (10/2)^2 = 5^2 = 25
x^2 – 10x + 25 = -21 + 25 = 4
(x – 5)^2 = 4
x – 5 = ±2
| x = 5 ± 2 → x = 7 or x = 3 |
Practice problems on completing the square
Q1. Solve for x by completing the square: x^2 + 4x – 5 = 0
Q2. Solve for x, but note that the lead coefficient is not 1: 3x^2 + 12x – 15 = 0
Q3. In the expression x^2 – 14x, what is the constant you need to add to turn it into a perfect square trinomial?
Frequently Asked Questions on Completing the Square
What is completing the square used for?
Completing the square is a very useful technique in algebra, which your child will use to solve quadratic equations that are hard or impossible to factor by hand and convert equations into vertex form. This skill will also be useful in geometry.
What does completing the square mean?
The simple completing the square definition is to take a quadratic expression and turn it into a perfect square trinomial, which is done by adding a specific constant. For example, this is the technique you would use to transform x^2 + 6x + 9 into a (x + 3)^2.
How to complete the square?
First, make sure that the main coefficient is 1. Then, move the constant to the other side of the equal sign. After that, take half of the middle coefficient, square it, and add it to both sides of the equation. Rewrite the left side as a perfect square.
Math & reading from 1st to 9th grade
Looking for homework support for your child?
Choose kid's grade
Math & Reading for Grades 1–9
Build real confidence for your child with a Brighterly math or reading tutor.
