Consecutive Angles: Definition, Types, Solved Math Tasks
reviewed by Jo-ann Caballes
Updated on January 9, 2026
In the world of geometry, understanding how angles relate to one another is one of the key skills your child needs to master. This is a skill they will use in many math topics, from parallel lines to polygons.
In this article, we will look into consecutive angles. We will break down their types, definition and theorem, examples, and some practice problems to put theory into practice.
What are consecutive angles?
To explain the consecutive angles meaning in the simplest way, these are angles that appear one after another (with specific rules). As the word consecutive means following in order, it’s a very suitable name too!
In geometry, your child is likely to come across these angles in two contexts.
- The first is in transversals, where two parallel lines intersect a third line. In this specific setup, consecutive angles are those on the same side of the transversal. Because of this, these angles are often referred to as consecutive same side interior angles, so don’t be confused if you come across this term.
- The next context in which consecutive angles are important is in polygons, particularly quadrilaterals such as parallelograms, rectangles, and trapezoids. Consecutive angles in a parallelogram are the angles located, again, on the same side or “edge” of the shape. The reason they are important in these shapes is that they add up to exactly 180°. We will talk about this in detail later in the article.
Don’t worry if this sounds confusing now, as it’s quite simple. The illustration below can give you a better idea of what consecutive sides and angles are.
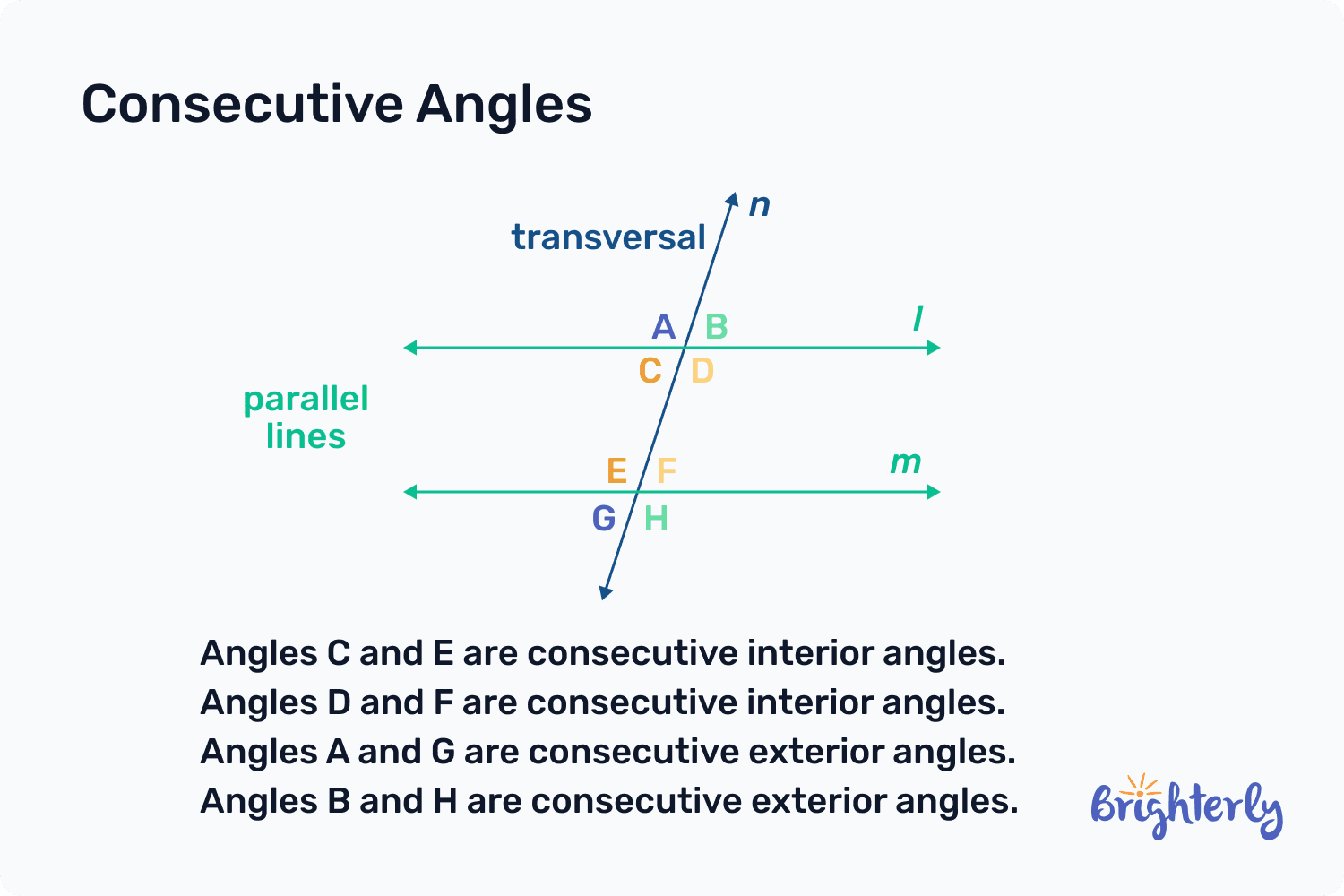
Consecutive angles definition
In geometry, we can define consecutive angles as a pair of angles that lie on the same side of a transversal and are between or outside two intersecting lines. They are often called same-side angles, because they lie on the same side of the line that cuts across the parallel lines.
Consecutive angles: Types
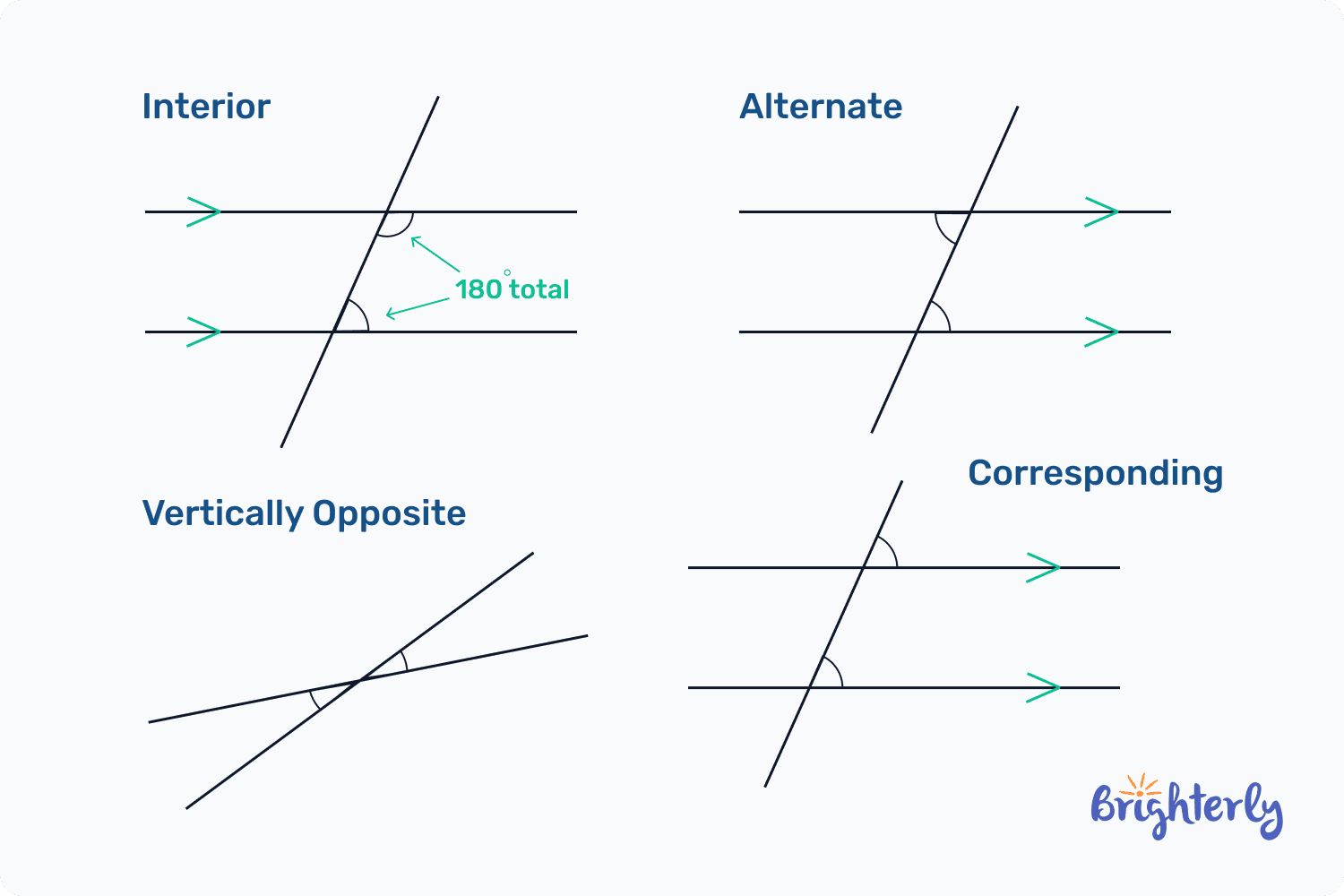
Despite all consecutive angles sharing the “same-side” property (by sitting on the same side of the transversal line), these angles are not the same. They have types, which we classify mainly by whether the angles lie inside or outside the two main lines. We call them consecutive interior angles and consecutive exterior angles. Knowing which type is which is critical if you want to understand the relationships between angles and the formulas governing them. Let’s look at each type in depth.
Consecutive interior angles
The first type is the consecutive interior angle, also called same-side interior angles, and is probably the most common type of angle your child will encounter in geometry.
According to the consecutive interior angles definition, this pair of angles is located within the interior region (on the same side of the transversal), which is the space “inside” when the transversal intersects the two parallel lines.
When you look at the interior angles in the image below, you will notice that these angles are facing each other. One important property of these angles is that if the two lines are parallel, the consecutive angles are supplementary. This means that their sum is exactly 180°. We wouldn’t be exaggerating if we said that this feature is the cornerstone of Euclidean geometry, as the supplementarity of angles is used to prove that lines are parallel or find missing measurements in shapes like parallelograms.
Consecutive interior angles examples
Let’s have a look at some examples of consecutive interior angles to give you a better glimpse of what is a consecutive interior angle is in practice.
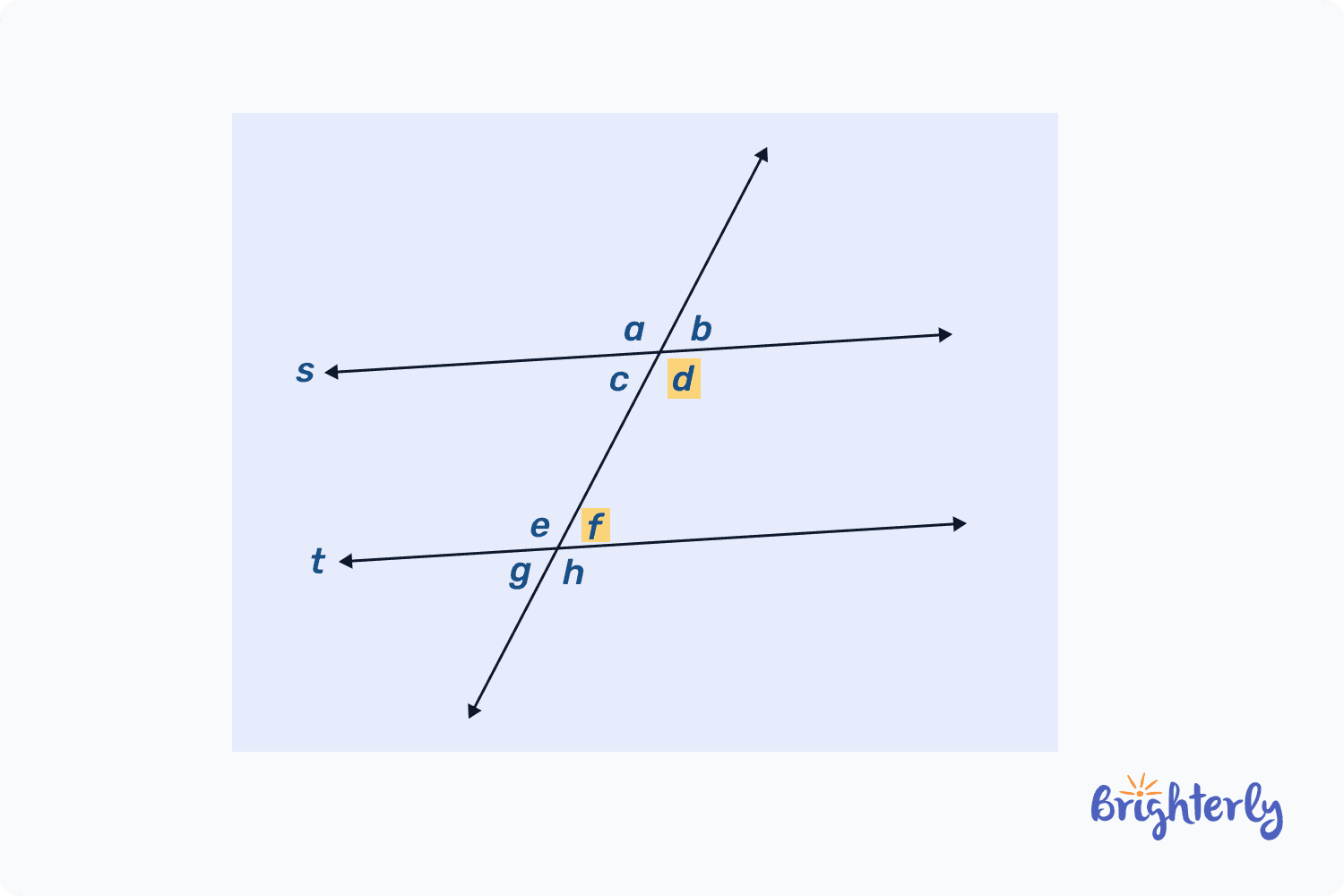
In the picture below, there are two pairs of these angles.
The first pair is angles d and f, which are formed on the right side of the transversal and on the inside part of the parallel lines. Because the lines are parallel, the measures of the angles add up to 180°.
The second pair is angles c and e. They are located on the left side of the transversal and share the remaining qualities of the first pair (located between parallel lines and adding up to 180°).
In the case of a consecutive interior angles example problem, if you are told that the angle a is 70°, you can be sure that the other angle is 110°.
Consecutive exterior angles
Now, let’s move on to the second type of angles, the consecutive exterior angles.
As you’ve probably guessed, exterior angles (also called same-side exterior angles) lie on the same side of the transversal and occupy the outer regions of the parallel lines. Just like the supplementary consecutive interior angles, the other type is also supplementary when the lines are parallel, adding up to 180°. If the sum of the two angles isn’t 180, it means the lines are not parallel and will eventually collide.
One challenge with these angles, especially for students who have just learn geometry, is spotting them, since they are located further apart than the interior angles. However, remembering the role that they still sit on the same side of the crossing line, one at the very top and one at the very bottom of the intersection area, can help greatly.
Consecutive exterior angles examples
As an example, let’s take the above image we used for the example of consecutive interior angles. Here, too, there are two pairs of exterior angles.
The first pair is angles a and g, which are located on the left side of the transversal and the outer sides of the parallel lines.
The second pair is, as you’ve probably guessed, the angles b and h. They sit on the outer sides of the parallel lines, but on the right side of the intersecting line.
As you can see, two parallel lines and one transversal form four exterior angles (two pairs of consecutive exterior angles).
Consecutive interior angles theorem
To deepen your understanding of consecutive angles, we need to look at the formal rules that govern them.
The property stating that if two parallel lines are cut by a transversal, then the pairs of consecutive interior angles are supplementary is known as the consecutive interior angles theorem. As you already know, supplementary angles in geometry mean that the sum of angles adds up to 180°. In the case of the example from the image we looked into,
- ∠c + ∠e = 180°
- ∠d + ∠f = 180°
This theorem is interesting also because it’s sort of a two-way street your kid can use to prove that the lines are parallel. This other theorem is called the converse of the consecutive interior angles theorem, which states that if we find a pair of same-side interior angles that add up to 180°, the lines are parallel.
Consecutive exterior angles theorem
In a similar fashion, the consecutive exterior angles theorem applies to the outer side of the intersecting line. This theorem states that when two parallel lines are intersected by a transversal, the resulting consecutive exterior angles are supplementary. In the case of the same example, we get
- ∠a + ∠g = 180°
- ∠b + ∠h = 180°
Much like the consecutive interior angles theorem, if we know that the angles are supplementary (or can prove they are supplementary), we can also prove that the lines are parallel. This theorem is also important if you only know the outside measurements of geometric figures, as it can help with calculating other measurements.
Consecutive angles in a parallelogram
While much of our discussion has focused on lines cut by a transversal, the concept of consecutive angles is equally vital when studying polygons, especially quadrilaterals.
Consecutive angles in a parallelogram are the angles that are located at the endpoints of the same side. We define a parallelogram as a shape with two pairs of opposite sides that are parallel; every side of the shape essentially acts as a transversal for the other two parallel sides.
The core rule for angles in a parallelogram is the same as for the other angle types we covered before. Namely, the consecutive angles in a parallelogram are supplementary. This means that the two angles that come one after another around the perimeter must add up to 180°. For example, if we moved clockwise around a parallelogram ABCD,
- ∠A and ∠B,
- ∠B and ∠C
- ∠C and ∠D
- ∠D and ∠A
would be consecutive. This is an incredibly useful property that can help your child understand the entire geometry of the shape, since if they know just one angle, they can determine all others. Additionally, the opposing angles in a parallelogram are equal, which further simplifies the calculations.
Consecutive angles: Solved math tasks
1. In parallelogram PQRS, ∠P = 115°. What is the measure of its consecutive ∠Q?
Solution: Since, according to the consecutive angles theory, the sum of the angles adds up to 180°, the solution is 180° – 115° = 65°
Answer:
| 65° |
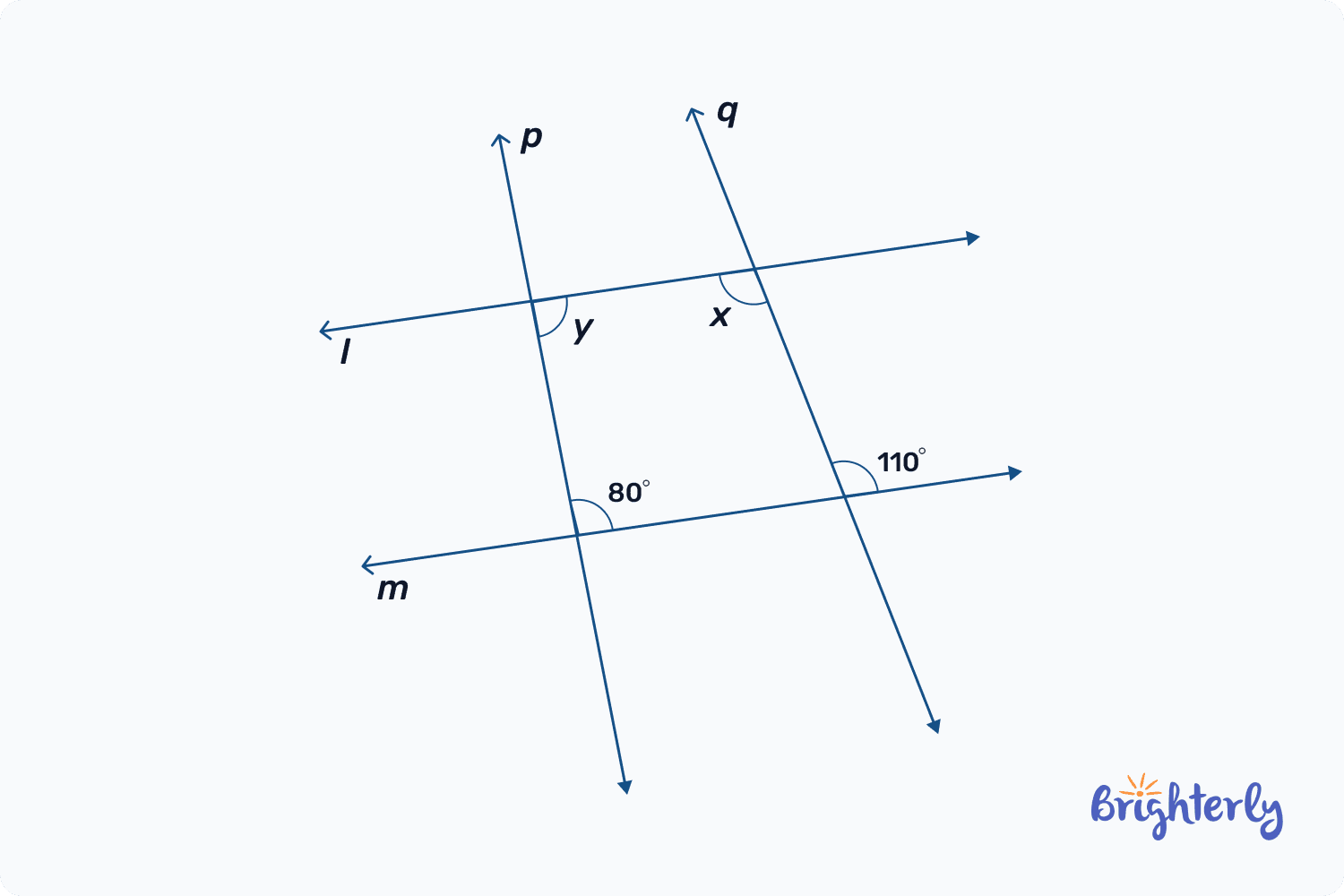
2. We have two parallel lines cut by a transversal. If ∠a = 80°, find the consecutive ∠g.
Solution: Since consecutive angles are supplementary, the solution is 180° – 80° = 100°
Answer:
| 100° |
3. One interior angle is 90°, and its same-side partner is 90°. Are the lines parallel?
Solution: Again, use the consecutive interior angles theorem. This is a rare case when the consecutive angles are congruent. However, since 90°+90° = 180°, the lines are parallel.
Answer:
| Yes, the lines are parallel. |
Consecutive Angles: Practice Math Problems
Frequently asked questions on consecutive angles
What is a consecutive angle?
Consecutive angles are a pair of angles that form when two parallel lines, which can also be at the end of the same side in a polygon, are intersected by another line (known as a transversal line). Consecutive angles are supplementary when the intersecting lines are parallel, and their sum is 180°
What are consecutive interior angles?
Consecutive interior angles are also known as the same-side interior angles. They are the pair of angles that form in the interior region between the two intersecting lines. They are located on the same side of the transversal line and are supplementary.
Are consecutive interior angles congruent?
Generally, no, they are not congruent. Consecutive lines can be congruent only when they are right angles (each at 90°). In the cases when the lines are parallel, these angles are supplementary rather than congruent, adding up to 180°.
What are consecutive angles in a parallelogram?
In a parallelogram, the consecutive angles are the pair of angles located at the endpoint of the same side. The reason behind this is that the opposite sides of parallelograms are parallel, so angles formed on the same side through an intersection are supplementary.
Are consecutive angles supplementary?
Consecutive angles are supplementary, but only in the case when the two lines intersected by a transversal are parallel. In this case, the sum of their measures is (whether you have exterior or interior pairs) is 180°. If the lines aren’t parallel, the consecutive angles are not supplementary.
Consecutive angles: Worksheets
Consecutive angles are a foundational topic in geometry; skipping or not fully understanding them can greatly hinder your kid’s geometry journey later on. In this article, we tried to explain the consecutive angles theorem, its types, and their usage clearly, in a way that is easy enough for your child to understand the idea and to see how exciting this topic is.
And now, it’s time to put the theory into practice! Have a look at the free related worksheets below, filled with interesting puzzles and problems, which can help your kid to further apply what they have learned.
- Lines and Angles Worksheets
- Missing Angles In Triangles Worksheets
- Pairs Of Angles Worksheets
- Properties Of Rectangles Worksheets
- Types Of Angles Worksheets
Winter Math & Reading Camp for Grades 1-9
Join Brighterly's Online Winter Camp to excel in math and reading.
Choose kid's grade
Winter Math & Reading Camp for Grades 1-9
Join our Winter Camp, boost your child's math and reading skills.
