• Math tutors
• /
• Knowledge Base
• /
• Fraction Greater Than 1 – Definition with Examples

Fraction Greater Than 1 – Definition with Examples

Camille Ira B. Mendoza

Updated on November 3, 2025

Fractions are an important and fascinating aspect of math, so we’re here to help you understand everything there is to know about them.

Today, we’re going to specifically cover fractions greater than 1. These are also known as improper fractions, and they can be presented in different ways.

Here, we’ll go over the fraction greater than 1 definition, its properties, and the difference between these and standard fractions. We’ll also show how to convert them and share some practice problems so you can test your understanding of this concept.

What are fractions greater than 1?

Fractions greater than 1 are fractions that represent a value larger than the number 1. This means they are a fraction where the numerator is greater than the denominator.

You’ll likely know by now that fractions represent part of a whole. For example, if you divide a pizza into 6 sections, you have 6 fractional representations of a pizza, and each slice represents ⅙ of the pizza.

However, if you had a pizza with a fraction greater than 1, you could have a 7th, 8th or even 9th slice, representing the fact that you have more than 1 pizza.

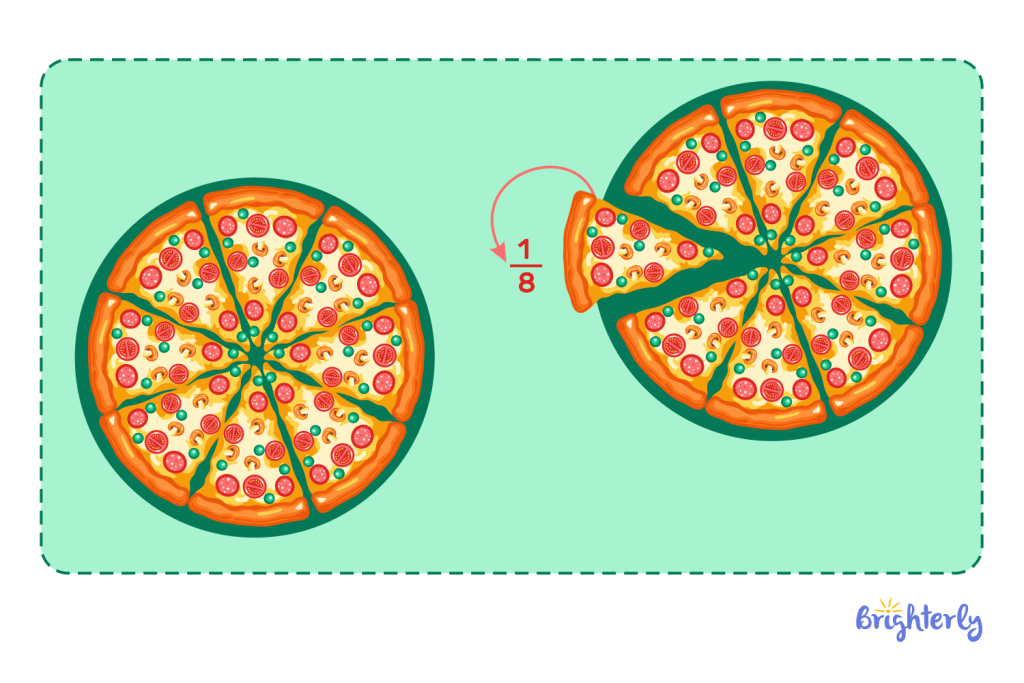
Properties of fractions

Fractions have a range of properties that make them a distinctive concept in math:

• If the numerator (top number) of a fraction is 0, the whole fraction is equal to 0
• You cannot have a fraction with a denominator (bottom number) of 0, because you cannot have smaller parts of 0.
• We can flip the numerator and denominator to create a new fraction value known as a denominator. For example, the reciprocal of ⅓ is 3/1
• Fractions can often be simplified by dividing the numerator and denominator by their greatest common factor. For example, 4/8 becomes ½ 

Properties of fractions greater than 1

Now, let’s look at the specific properties of fractions greater than 1:

• Fractions greater than 1 will always have a numerator that is larger than the denominator
• These fractions can be presented as an improper fraction (with a numerator larger than the denominator) or as a mixed fraction (a whole number accompanied by a fraction)
• You can also plot fractions greater than 1 on a number line, providing you have lines representing portions of numbers between each whole number.

Difference between fractions greater than 1 and fractions

The main difference between fractions greater than 1 and fractions is the quantities they represent. A standard fraction represents a number equal to, or less than, 1, while fractions greater than 1 will always represent values larger than 1.

Representing fractions greater than 1

There are two different ways you can represent fractions greater than 1:

• As an improper fraction: Your numerator would be bigger than your denominator to represent that the whole fraction’s value is larger than 1
• As a mixed fraction: Here, you’d represent it as a whole number and a fraction, with the whole number representing the fact the fraction’s value is larger than 1

If we use the example of 9 parts out of 6, you can either represent this as an improper fraction, which would be 9/6, or as a mixed fraction, which is 1 3/6 (you can further simplify to 1 ½).

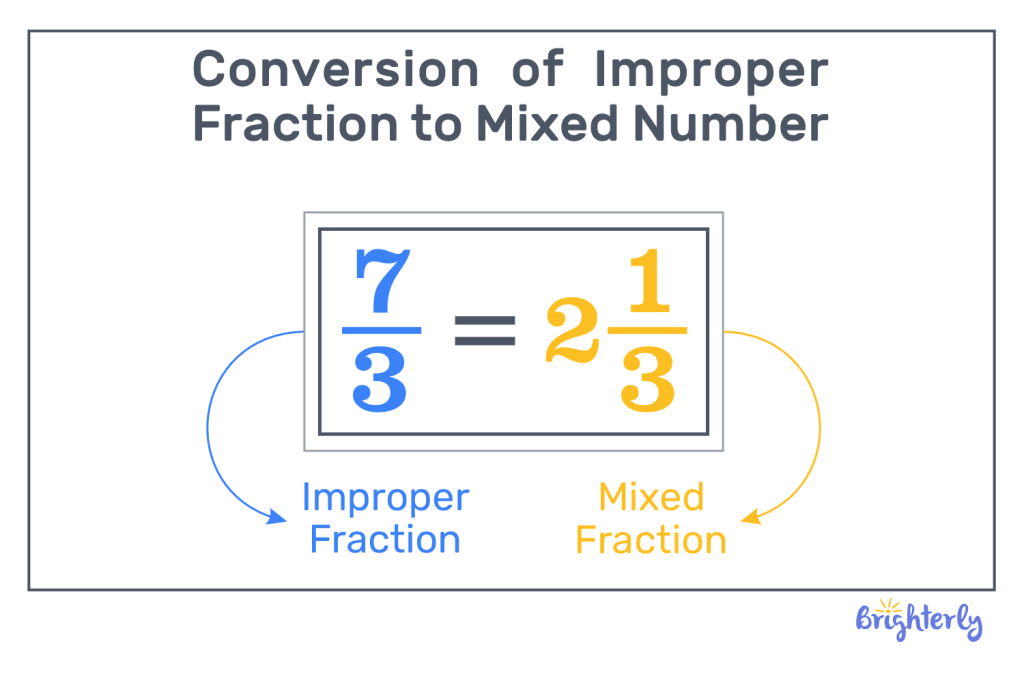
Converting fractions to fractions greater than 1

To convert a fraction to a fraction greater than 1, you simply need to increase your numerator until it is larger than the number 1. Let’s look at an example of which fraction is greater than 1. If you have the fraction ⅘, changing the numerator to 6 to make 6/5 makes it a fraction greater than 1.

Converting fractions greater than 1 to mixed numbers

The quickest way to convert fractions to fractions greater than one in a mixed fraction representation is to divide your numerator by your denominator. Your quotient will be your whole number, and any remainder will become your new numerator.

Let’s look at an example. If you have the fraction 8/3, your mixed fraction would be 2 ⅔, because you can divide 8 by 3 twice, with a remainder of 2.

Math tutors

Improve your child’s math skill today with Brighterly

Let them be at the top of their class.

Book free lesson

Fractions greater than 1: Practice problems

Now, it’s time to try your hand out at some questions around fractions greater than 1. These practice problems will help you prepare for exams in school, as well as answering questions in your math class. Work out the answers mentally or write them down with a pen and paper.

• You have the improper fraction 8/2. Convert this to a mixed fraction.
• You have 7/6 of a pizza, and you eat ⅚ of it. How much pizza do you have left?
• Which fraction is greater: ⅞ or 8/7?
• Convert the fraction 9/10 so it is a fraction greater than one

Conclusion

Fractions greater than 1 are just one part of the bigger picture of fractions in math. Now that you know all about them, you can more confidently identify, work with and convert fractions greater than 1!

Fractions greater than 1: Frequently asked questions

What is a fraction greater than 1?

A fraction greater than 1 is a fraction that represents a value greater than the number 1. This means it can be expressed as an improper fraction (a fraction with a numerator larger than its denominator) or a mixed fraction (a whole number combined with a fraction).

What fractions are greater than 1?

There are lots of fractions that are greater than 1, for example 3/2, 6/5 and 9/4 are all fractions greater than 1. Any fraction that has a numerator larger than a denominator, or a whole number combined with a fraction, is a fraction greater than 1.

What is the difference between a fraction and a fraction greater than 1?

The difference between a fraction and a fraction greater than 1 is the value they represent. A fraction will represent a part of a whole, meaning their value will be smaller than, or equal to, the number 1. A fraction greater than 1 represents a value larger than the number 1.

How to convert a fraction to a fraction greater than 1?

To convert a fraction to a fraction greater than 1, you need to increase the numerator so it’s bigger than the denominator. If we look at what fraction is greater than ½, we can change the 1 to 3, making it 3/2 which is a fraction greater than 1.

Camille Ira B. Mendoza

35 articles

I am a seasoned math tutor with over seven years of experience in the field. Holding a Master’s Degree in Education, I take great joy in nurturing young math enthusiasts, regardless of their age, grade, and skill level. Beyond teaching, I am passionate about spending time with my family, reading, and watching movies. My background also includes knowledge in child psychology, which aids in delivering personalized and effective teaching strategies.