Linear Measurement – Definition with Examples
Updated on November 27, 2025
Whenever we measure the length, width, or height of an object, we are taking a linear measurement. So not only are linear measurements important in many school subjects, but they are also key to our wider lives!
Understanding the topic sets you up for a successful geometry learning journey. So here, we’re going to cover the definition of these measurements, their properties, conversions, and linear measurement examples. We’ll also give you some practice questions so you can apply your understanding.
What is linear measurement?
A linear measurement is a straight line that stretches between two points, i.e., a distance measurement. Whenever we measure a full or partial object, we are carrying out a linear measurement. There are different types of linear measurement, including height, width, and length.

Definition of linear measurement
The linear measurement definition states it’s the distance between two points or objects that can be measured. It must be in a straight line to be considered a linear measurement. We have different types of linear measurements we can carry out:
- Height: the measurement from the bottom to the top of an object
- Width: the shortest dimension of an object, often measuring an object from side to side or front to back
- Length: the longest dimension of an object, which can also be measured front to back or side to side
Definition of units in linear measurement
When you perform a linear measurement, you use specific units of measurement. These are units of distance and can include:
- Millimeters
- Centimeters
- Meters
- Kilometers
- Inches
- Feet
- Miles
Some of these linear units of measurement (millimeters, centimeters, meters, and kilometers) form part of the metric system, while others (inches, feet, and miles) are part of the imperial system.
Properties of linear measurement
Like many other geometric concepts, linear measurements have properties that make them stand out:
- Linear measurements are a scalar quantity, meaning they have magnitude but not direction
- These measurements are invariant, which means that no matter the orientation and position of your object, its linear measurement will stay the same
- Linear measurements are transitive, meaning that if point A and B are the same distance apart as point B and C, point A and C are the same distance apart
Properties of units in linear measurement
You may be interested to know that the units of linear measure also have distinct properties!
- All linear measurement units are standardized, which means they are clearly defined and unchanging
- Units in the metric system are scalable and work to the base-10 system, meaning conversions are based on factors of 10
Differences between units of linear measurement
The main differences between units of linear measurement come from their respective systems and sizes. Centimeters, inches, and millimeters are considered small measurements, while meters, miles, and kilometers are larger measurements.
Metric units are scalable in the base-10 unit, while units in the imperial system don’t convert quite as smoothly.
Equations involving linear measurements
There are many formulas you might use in math class that are related to linear measure, including:
- Finding the perimeter of a square: Perimeter = side x 4
- Distance, rate, and time: Distance = rate x time
- Finding the perimeter of a rectangle: Perimeter = 2(length) + 2(width)
- Slope intercept form: y = mx + b
Writing equations involving linear measurements
When writing equations involving linear measurements, you need to be aware of what your variables represent. For example, you’ll need to know your side lengths and widths when calculating the perimeter of a triangle. Similarly, if you’re carrying out the slope-intercept form, you must know that m represents your slope and b is the y-intercept.
Converting different units of linear measurement
Sometimes you may be required to convert between different units of linear measurement. This is easy with measurements in the metric system, as they work to a base-10 system. For imperial measurements, a chart can be handy.
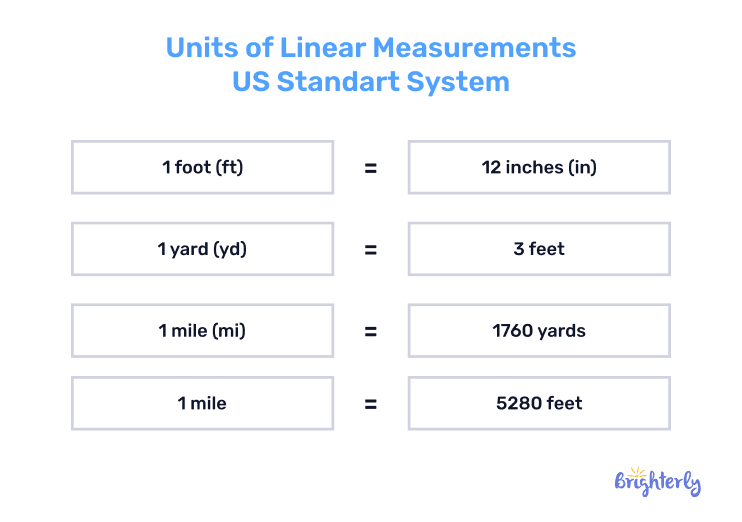
Practice problems on linear measurements
Now, it’s time to try your hand at some practice problems. These questions will help you test your understanding of linear measures!
- You have a rectangle with a length of 5 cm and a width of 3 cm. Work out the perimeter.
- How long is a 5k run in miles?
- If you have a 7.5-inch-long pencil, how long is it in feet?
Conclusion
Now, you can consider yourself a master of linear measurement! Learning to measure items in a linear fashion is a key skill not only in math and geometry, but in subjects like science, and in our real lives. Now, go forth and apply your newfound knowledge!
Frequently asked questions on linear measurement
What is a linear measurement?
Linear measurement is the distance from one point or object to another. It can include key measurements like height, width, and length.
What are the units of linear measurement?
Units of linear measurement include:
- Millimeters
- Centimeters
- Meters
- Kilometers
- Inches
- Feet
- Miles
- Yards
Some may ask, “What are the five linear measurements?”, but as you can see, there are more than five measurements!
How to do a linear measurement?
To do a linear measurement, you would use a measuring device like a ruler or tape measure to assess the distance between two points or objects. You’d measure this in units like centimeters, meters, or inches.
What are the two systems of linear measurement?
The two systems of linear measurement are the metric system and the imperial system (also known as the US customary system). The metric system includes millimeters, centimeters, and meters and is used by most of the world. The US uses the imperial system, which covers feet, inches, yards, and more.
How do you convert between different units of linear measurement?
Conversion between different units of linear measurement depends on what system they’re in. Metric units can be converted in multiples of 10 — i.e., 10mm is 1cm, and 100cm is 1m — whereas in the customary system, or cross-system, you’ll need conversion formulas.






