Negative Slope: Definition, Graph, and Solved Examples
reviewed by Jo-ann Caballes
Updated on November 15, 2024
We express relationships between two quantities through lines and slopes and these slopes can be positive, negative, zero, or undefined.
Here, we discuss negative slopes. We explain what it is through the negative slope definition and negative slope examples. We encourage learners to understand it more by giving practice questions and helpful worksheets.
What is a negative slope?
The negative slope is a downward trend of a line moving from left to right. It means a negative relationship between two values — when one value goes up the other one comes down.
What does a negative slope look like?
A negative slope is a line that has a falling appearance from the left to the right. It also forms an obtuse angle at the point of intersection with a straight line. This is because the downward slope of the line when it meets with the vertical line, forms an angle greater than 90 degrees.
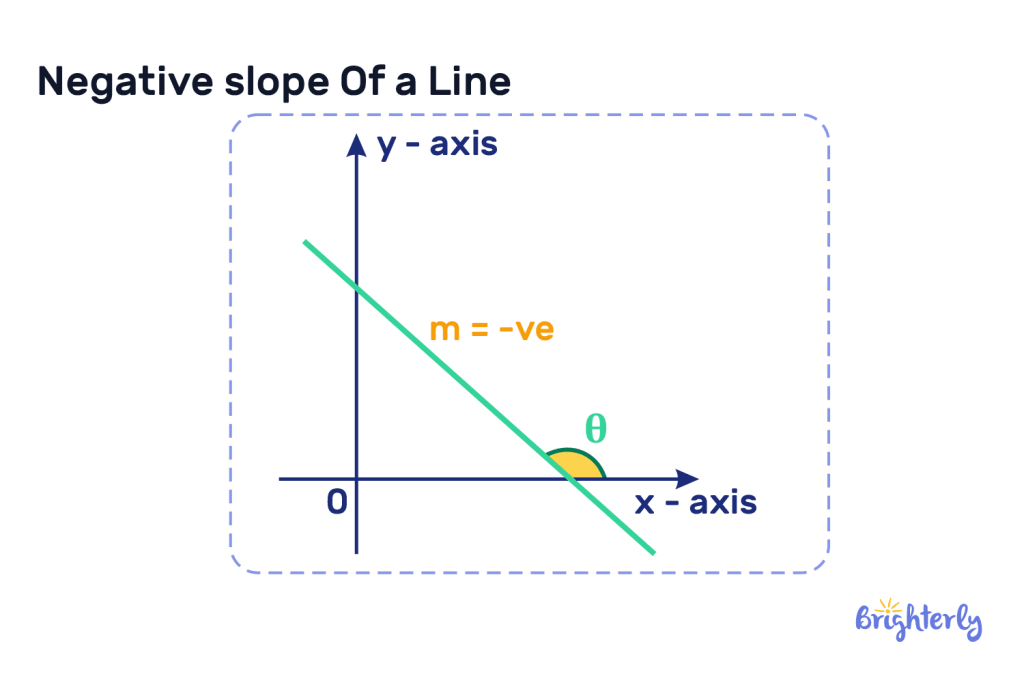
Negative slope example
If you pay close attention, you will notice the presence of negative slopes around you. Here are some examples:
- When walking you may notice a downward road or hill that is different from the straight road.
- If graphed, a person’s weight loss journey will show a negative slope to show weight loss.
- Also if graphed, we can observe a negative slope when monitoring the weather temperatures as we move from summer to winter conditions
- A playground slide has a negative slope because it goes from up at the left to down at the right.
Negative and positive slope
To understand the positive slope vs negative slope, let’s first explain what a slope is:
A slope refers to the change in y in relation to the change in x.
The negative slope occurs when the relationship between the two variables is negative, and the positive slope occurs when the relationship between the two variables is positive.
Negative slope: Negative rise over run ratio
We represent the slope with the symbol “m”, and as we discussed above, it is the change in y divided by the change in x.
Change is represented as Δ
Therefore, the formula for slope is: m = Δy/Δx
This is known as the rise over run ratio which can be positive, negative, or even zero. It explains that the change in the y-axis will affect the x-axis and vice versa.
When the slope is negative, it means the change in rise, i.e. the change in y is negative and the change in run (change in x) is positive which causes a negative value for the slope.
Therefore, the negative slope equation is: m = –Δy/Δx
Negative slope graph
It is established now that the negative slope is the inclined appearance of a line from left to right. It also shows that as the y value decreases, the x value increases. If the line moves upward from left to right, it becomes a positive slope.
Here’s an example of the negative slope on a graph:
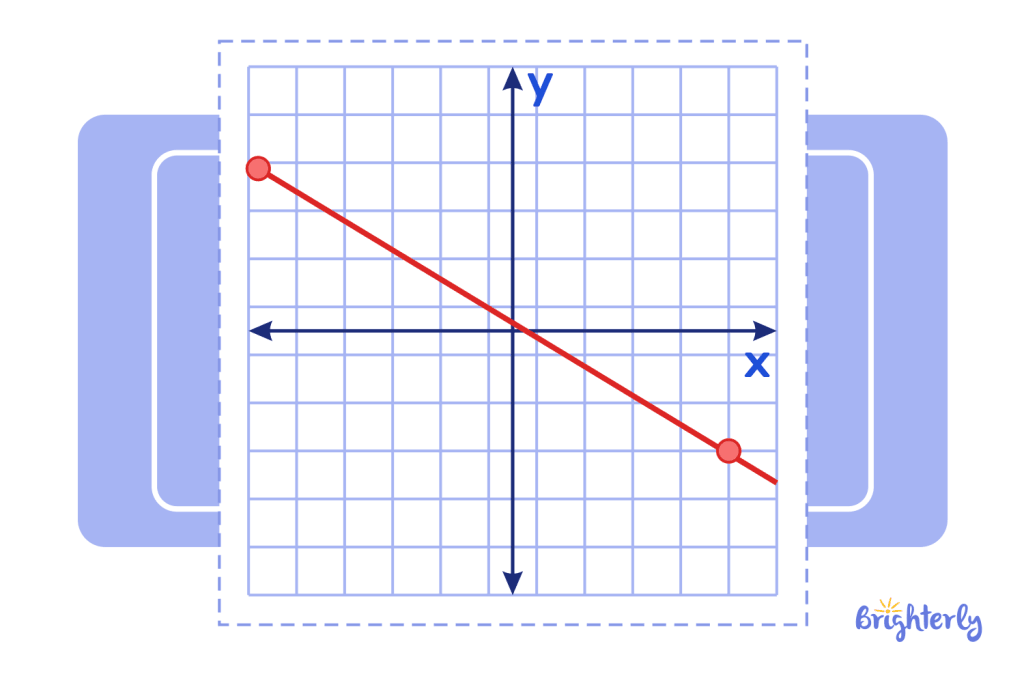
When observed, we notice that the negative line on the graph is the blue line because it matches the description of how a negative slope looks.
Note that a negative slope on a graph does not make it a negative graph because there can still be positive and negative lines on the graph. It depends on how much data is plotted.
How to calculate a negative slope?
There are various ways to find out if a line is a negative slope. Here are some of them:
1. The two points method:
m = (y2 – y1)/(x2 – x1).
Here, we are provided with details about the coordinates of the points in the line, so we minus the y-coordinates and the x-coordinates, and then we divide the results. For instance, when x1 is 3, y1 is 5, x2 is 7, and y2 is 4, here is how we’d calculate it using this method:
m = (4 – 5) / (7 – 3) = –1/2
m having a negative value of –1/2 means the line has a negative slope.
2.The equation of a line method:
The equation of a line can be presented in various forms. If we are presented with the standard form of ax + by = c, we reconvert this equation to the slope-intercept formula to find out if the slope is negative.
For example, if the equation of the line is 4x + 9y = 7.
When changed to the slope-intercept formula that is y = mx + c, it becomes:
9y = —4 x + 7
Then, we divide both sides by 9 to get y alone
9y/9 = -4/9x + 7
y = -4/9x + 7
Remember that m = slope of the line and since m in the equation is -4/9, we can say that the equation of the line, 4x + 9y = 7, is a negative slope.
3. The angle method:
We use this method when we know the angle that the line makes with the x-axis. We convert the angle to θ = 90º + α when m = tan (θ).
For instance, when a line forms an angle of 150º, we solve it thus:
θ = (90 + 60), therefore,
m = tan (90º + 60º ) = –1/√3 = –0.577.
This means the slope is negative.
Solved Math Tasks: Examples
Solved math problem 1
A line has the following coordinates, (9, 7) (6, 3) what is the slope of the line?
Answer
x1 = 9
x2 = 6
y1 = 7
y2 = 3
When substituted into the formula, it becomes:
m = (3 – 7)/ (6 –9)
| m = –4/ –3. |
In mathematics, when negative divides negative, the answer becomes positive. Therefore, -4/ -3 becomes 4/ 3 which means the line is positive and not a negative slope line.
Solved math problem 2
Amber and Jay both have lemonade stands. She increases her prices and notices that sales decrease. Jay, however, finds that as he increases his prices, his sales also increase.
If expressed as a line, what types of slope would both of these instances form?
Answer
|
If we represent y with sales and x with prices, the first instance would form a line with a negative slope because y decreases as x increases. The second instance, however, is a positive slope because the sales increase even though the price is also up, meaning the line moves upward from left to right. |
Solved math problem 3
The equation of a line is 9x + 7y = 4, is it a positive slope or a negative slope?
Answer
We convert the equation to y = mx + c as follows:
7y = -9x + 4
7y/7 = -9/ 7x + 4
y = -9/ 7x + 4
m = -9/7
| The line, 9x + 7y = 4 is a negative slope. |
Negative Slope: Practice Math Problems
Negative Slope: worksheets
Learn more about the positive slope vs negative slope and linear algebra with Brighterly’s free worksheets:
Math homework help for grade 1-8
Get the homework support your child needs!
Choose kid's grade
Math Program
Boost Your Child's Math Abilities! Ideal for 1st-8th Graders, Perfectly Synced with School Curriculum!
