• Math tutors
• /
• Knowledge Base
• /
• One-Step Equations: Definition, and Solved Examples

One-Step Equations: Definition, and Solved Examples

Jessica Kaminski

reviewed by Jo-ann Caballes

Updated on October 28, 2024

Welcome to another informative article at Brighterly, where we make learning math straightforward and exciting!

Today, we’re delving into the world of algebra and taking a look at one-step equations.

These equations are a fundamental part of both math and algebra. Understanding them is the starting point for working with more complex equations and expressions.

In this article, we’ll cover the one-step equation definition, how to solve one-step equations and share examples. We’ll also give you a chance to solve one-step equations practice problems and provide engaging math worksheets so you can test out your knowledge.

What is a one-step equation?

Put simply, a one-step equation is any algebraic equation that can be solved in a single step. One-step equations can be solved either through addition, subtraction, division or multiplication. We cover the full definition of the one-step algebraic equation below.

One-step equation definition in math

One-step equations, also known as single-step equations, are solvable in one step and are categorized as algebraic expressions. 

One-step equations will always include a variable (an unknown number represented by a letter) and a constant (an unchanging number with no variables), and they can also include coefficients (a number placed before a variable that multiplies the variable). 

By solving one-step equations, we naturally solve the value of the variable. For example, 7x + 5 = 19 is a one-step equation. To solve this equation, we inverse the operation to work out the value of x. We simply inverse the operation – so here, our equation becomes 19 – 5 = 7x. 19 minus 5 is 14, then we divide 14 by 7 to get the value of x. 14 ÷ 7 = 2, therefore x = 2.

The final term in a one-step equation will always be a constant.

How to solve one-step equations?

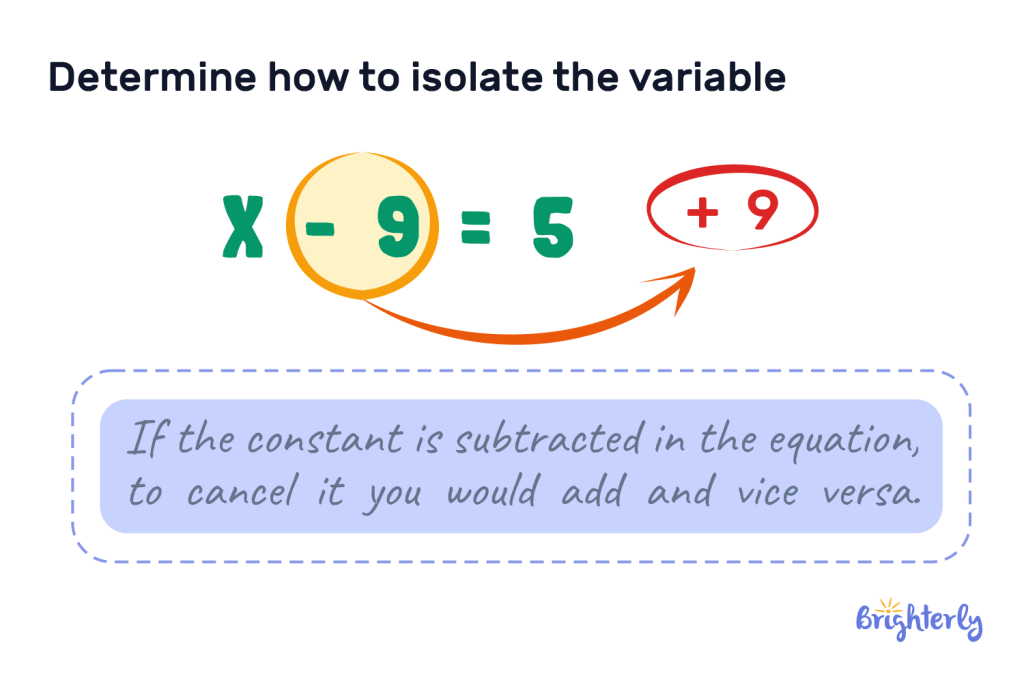
Solving one-step equations is easy, you simply need to inverse the operation. This means that you perform the opposite of the operation in the equation. So, in terms of how to solve a one-step equation:

• If your equation has an addition sign, you subtract
• If your equation has a subtraction sign, you add
• If your equation has a multiplication sign, you divide
• If your equation has a division sign, you multiply

One-step equation examples

Here, we’ll provide some examples of one-step equations. There are three main types of one-step equations that we will provide examples of:

• One-step equations with integers
• One-step equations with decimals
• One-step equation with fractions

One-step equations example 1: integers

One-step equations using integers will only feature integers as constants or coefficients, in addition to variables.

Here are some examples of simple one-step equations using integers:

• 5x + 2 = 17
• y ÷ 4 = 3
• x2 = 12

Here, all of the constants and coefficients featured in the equations are integers – i.e. whole numbers. There are no fractions or decimal numbers in one-step equations with integers.

One-step equations: example 2: decimals

One-step equations using decimals will use numbers with decimal places as constants, in addition to variables.

Here are some examples of simple one-step equations using decimals.

• 0.5 + x = 1.25
• 0.2 x y – 1
• 1.5 x y = 4.5

There are no fractions or integers in one-step equations with decimals.

One-step equations example 3: fractions

The one-step equation with fractions will use fractions as constants, as well as variables.

Here are some examples of simple one-step equations using fractions:

• 5x/6 = 6/9
• y/4 = 3
• x 1 ⅜ = 3

There are no integers or decimal numbers in one-step equations with fractions.

One solution definition in math

One solution in math is related to one-step algebraic equations. One solution means that there is only one value for the variable for the equation to be true. For example, in the one-step equation 7 + y = 13, there is only one possible value that y can be, which is 6. Therefore, there is only one solution. This is true of all one-step equations.

Rules for one-step algebraic equations

There are specific rules that define one-step algebraic equations because not all of them are one-step equations. These rules are:

• They must be solvable within one step
• They will always include at least one constant and one variable
• They can also include coefficients
• In order to solve a one-step algebraic equation, you need to reverse the operation of the equation

Solved math tasks: examples

Ready to put your knowledge of one-step equations into practice? We’ve put together some solved math tasks – simply try your hand at solving one-step equations featured below, then check back in to see if you’ve got them right. Check out these one-step equations examples with answers.

Solved math task 1

Solve the following one-step algebraic equation:

x + 17 = 21

Answer:

To work out the value of x, you need to inverse the operation. Therefore, x + 17 = 21 becomes 21 – 17 = 4.

Solved math task 2

Solve the following one-step algebraic equation:

15 ÷ y = 3

Answer:

To work out the value of x, you need to inverse the operation. Therefore, 15 ÷ x = 3 becomes 3 x y = 15, and we know 3 goes into 15 5 times, so we know y is 5. 

Solved math task 3

Solve the following one-step algebraic equation:

x – 0.5 = 0.2

Answer:

To work out the value of x, you need to inverse the operation. x – 0.5 = 0.2 becomes 0.5 + 0.2 = 0.7.

One-step equations: practice math problems

One-step equations: worksheets

Now that you know everything there is to know about one-step equations, it’s time to put that knowledge into practice! Download our fun, free math worksheets and enjoy challenging, game-based exercises to hone your knowledge.

• One-step equation worksheets
• Equations and inequalities worksheets
• Algebra worksheets
• Evaluating expressions worksheets

Jessica Kaminski

70 articles

Jessica is a a seasoned math tutor with over a decade of experience in the field. With a BSc and Master’s degree in Mathematics, she enjoys nurturing math geniuses, regardless of their age, grade, and skills. Apart from tutoring, Jessica blogs at Brighterly. She also has experience in child psychology, homeschooling and curriculum consultation for schools and EdTech websites.