Patterns – Definition With Examples
Updated on January 9, 2026
The abstract world of mathematics is an exciting one, with so many hidden, fascinating topics to explore. Today, we will do just that by diving deep into the realm of math patterns.
Patterns are all around us, from daily routines structuring our lives to the beats of our favourite music. And much like in life, in mathematics too, patterns establish a predictable framework and order, this time in the world of numbers.
In this article, we will look into what patterns are, what are some of the most common patterns in mathematics, explore their types and some exciting pattern examples, and so much more.
Patterns definition
Patterns are something children encounter and learn to recognize very early. From the alternating colors of a striped shirt to the predictable sequence of “play time, snack time, nap time”, our brains are wired to look for patterns everywhere and seek predictability and regularity.
In the world of mathematics, this instinct becomes a discipline. The definition of pattern in math is an ordered set of numbers, shapes, or objects that follow a specific, logical rule. This rule is what transforms a random collection of mathematical items into a logical sequence we can find and understand.
One way your child can think of patterns in math is as a mathematical code. Once they crack the code by identifying the specific pattern, they gain the power of prediction: they no longer need to see the next item in the sequence to know that it is. Math pattern examples they encounter can range from simple problems like realizing that every number in a list is 5 more than the last, to the fractal geometry of snowflakes.
The great thing about the pattern concept, both in math and in life, is that it allows us to look beyond numbers in isolation and see the big picture of how values interact and change. This way, by studying these patterns, your child will understand the logic of what they are doing instead of simply calculating the answers.
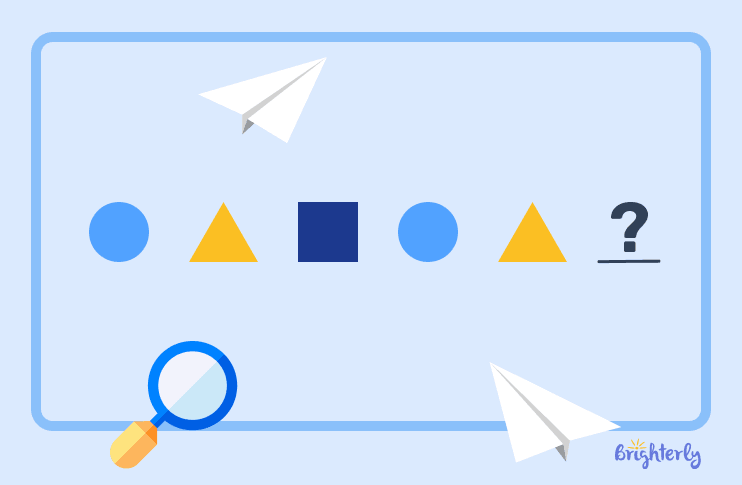
Finite patterns
One way we distinguish patterns math is by how long they last, generally categorizing them into finite and infinite patterns.
A finite pattern, as you probably have guessed, is a sequence that has a definite beginning and a clear end. This type of pattern contains a fixed number of elements. You can think of a finite pattern like a sentence, where we have a first word and a last word, with a set number of words. In math, an example of a finite pattern could be a short sequence of shapes, or the sequence {10, 20, 30, 40, 50}, as it stops exactly at 50.
Infinite patterns
In contrast, an infinite pattern is a sequence that continues forever and has no final term. The classic example of an infinite pattern is the set of natural numbers, the numbers we know and use, which start at 1 and go on forever (1, 2, 3, 4, 5, …). In this sequence, no matter how large the number is, you can always add 1 to it and get an even bigger number. In these patterns, we can apply the same rules over and over again, theoretically until infinity, and always get the correct answer. Each infinite pattern example helps us understand and appreciate the vastness of our number systems.
Rules of patterns
All patterns have rules. Otherwise, they wouldn’t have been patterns in the first place, but rather chaotic sets of numbers and shapes. Pattern rules are their “instruction manuals”, which, once you find them, the entire sequence starts to make sense. Below, we look at the three most common patterns in math.
Repeating pattern
The repeating pattern in math is the sequence, where a core group of elements appears over and over again in exactly the same order. We encounter repeating patterns everywhere, from nature to art to music. For example, the rule of the sequence A, B, C, A, B, C, A, B, C, A, B, C, A, B, C would be to repeat the sequence A, B, C indefinitely.
Growing pattern
Next up is the growing pattern rule. In this type of pattern, we can see the items in the sequence increase by value or size in a predictable way. Every new term is larger than the one before it, but the growth rate they go through is not random. Instead, it follows a rule that specifies how much we add to each element at each step. The rule can be as simple as adding + 3 to every element, or more complex, like the Fibonacci sequence we will explore later in the article.
We use growing patterns everywhere in our lives, from visualizing data trends to calculating interest.
Shrinking pattern
Shrinking patterns are the exact opposite of growing patterns. We also sometimes call them decreasing patterns. In the patterns following this rule, the value or size of each item decreases as the sequence goes on. The shrinking, naturally, follows certain rules, which will tell your kid how much they need to subtract or divide by at each step. 100, 90, 80, 70, … is a simple example of a shrinking pattern, where the rule is to subtract 10 from the previous number.
Types of patterns
The rules of patterns tell us how the sequence will behave. There are different kinds of patterns, the pattern types, which are the building blocks of each pattern. Understanding which pattern type they are dealing with will be the first step for your child to crack the code of the sequence and solve it. The three types of patterns we deal with in mathematics are the shape, letter, and number patterns.
Shape pattern
Shape patterns, also called visual or geometric patterns, involve creating a sequence using physical forms. These types of patterns are the ones we learn as children by playing with wooden blocks of different shapes and sizes.
Patterns in shapes can be repeating, like squares followed by circles, growing, such as a small triangle that gets larger, or decreasing. You can find examples of shape patterns in architecture and design.
Letter pattern
In letter patterns, we use the alphabet to create sequences. Your kid can come across these patterns in logic puzzles. Letter pattern rules can range from simple repetitive rules like A, B, A, B, or more complex rules like skip-counting. For example, if you see the sequence A, C, E, G, the pattern skips one letter between each term.
If your child is just learning what is pattern in math, you can use letter patterns as a bridge between the shape patterns and more abstract number patterns.
Number pattern
Number patterns are the most common type of patterns your kid will interact with in mathematics. These patterns use operations (addition, subtraction, multiplication, and division) to move from one term to the next. Because of this, number sequences are foundational for algebra.
When working with these patterns, students need to find the mathematical formula that predicts the future numbers. This can be simple sequences like 2,4,6,8, where they need to add 2, or more complex 2,4,8,16, where they need to multiply each number by two to get the next number, and many more complex patterns examples.
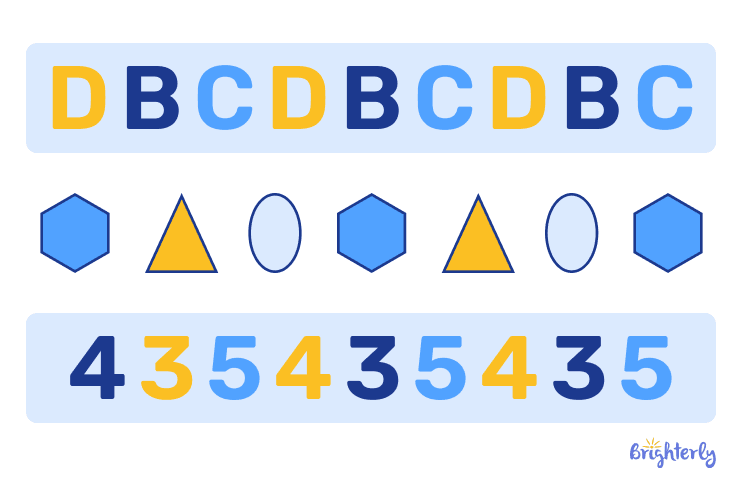
Number patterns types
Number pattern type, in turn, has three subcategories. Let’s look at them.
Arithmetic pattern
The arithmetic pattern, which is also known arithmetic sequence, is quite a simple one. In this pattern, the difference between the two consecutive terms is always the same. We call this difference the “common difference. So, to find the next number in an arithmetic pattern, your child needs to simply add or subtract the same value every time.
For example, in the sequence 3, 7, 11, 15, 19, 23,…, the rule is to add 4 every time. Unless specified differently, this sequence is infinite and can go on forever.
Geometric pattern
Next up is a geometric pattern. In this pattern, the ratio between the consecutive terms remains constant, as each number in the sequence is obtained by multiplying (or dividing) by the same fixed value, say, by 4. We call this fixed number a common ratio.
The difference between arithmetic and geometric patterns is that in the case of geometric, you use multiplication and division instead of addition and subtraction. Because of this, geometric patterns generally grow and shrink faster than arithmetic ones.
For example, in the sequence 2, 8, 32, 128, 512, … the rule is to multiply each number in the sequence by 4 to get the next number.
Fibonacci pattern
The Fibonacci sequence is the most famous and beautiful sequence in all of mathematics. Unlike the others, this pattern is created by adding the two previous terms together to get the next one. It usually starts with 0 and 1.
The sequence is 0, 1, 1, 2, 3, 5, 8, 13, 21, 34…, until infinity. The rule is 0 + 1 = 1, 1 + 1 = 2, 1 + 2 = 3, 2 + 3 = 5, and so on.
You will come across the Fibonacci sequence not only in math, but in art, architecture, and nature. You can find Fibonacci numbers in the spiral of a seashell, the arrangement of pinecone scales, and the number of petals on many flowers. This truly is a fascinating sequence.
Solved examples on patterns
1. What is the rule of the pattern 7, 12, 17, 22, …? Find the next two terms.
Solution: We can see that this is an arithmetic pattern. To find the difference between two consecutive terms, let’s subtract the small number from the large number: 12 – 7 = 5, 22 – 17 = 5. We subtract because we can see that this is a growing pattern. So, the rule is adding 5 to each consecutive element.
Answer:
| Adding 5, the next elements are 27 and 32. |
2. What is the rule of the pattern 2, 6, 18, 54, …? What will the next term be?
Solution: In this growing pattern, the gap between numbers is not the same, as 6 – 2 = 4, but 18 – 6 = 12. So, this is not an arithmetic pattern. Instead, we check by division: 6 /2 = 3, 18/6 = 3. So, the rule is to multiply each consecutive number by 3.
Answer:
| Rule is to multiply by 3, the next element in the sequence is 162. |
3. What is the rule of the pattern C, F, I, L, …? What are the next two terms?
Solution: Let’s look at the gap between the letters in the alphabet. Between C and F, two letters are skipped (D and E). Between F and I, two more letters are skipped (G and H). Since the gap is consistent, we can be certain that the rule is to skip two letters each time.
Answer:
| Skipping two letters; next elements are O (we skip M and N) and R (we skip P and Q). |
Practice questions on patterns
- What type of pattern does the sequence square, circle, triangle, square, circle, triangle follow? And what pattern type is it?
- What is the common difference in the arithmetic pattern: 14,21,28,35,…?
- Which rule describes the following shrinking pattern: 80,40,20,10,…?
- In the Fibonacci sequence (0, 1, 1, 2, 3, 5, …), what is the next number?
Conclusion
Our brains are wired to seek patterns everywhere, and it’s not a coincidence. Patterns go far beyond a simple list of numbers or shapes. They are what give our works their structure. That’s why we at Brighterly believe that when kids learn to spot patterns, they aren’t just doing math, but are learning to make predictions for the future and become more logical thinkers. So, we hope that this article helped to open the door to the fascinating world of mathematical patterns.
Frequently asked questions on Patterns
What is a pattern?
A pattern is an arrangement of numbers, shapes, letters, and other elements that follows a logical and predictable order. Each pattern has a specific rule that dictates how the sequence starts and continues, and by identifying that rule, students can predict the next element in the sequence.
How are patterns used in the real world?
Patterns are everywhere around us. We use them in architecture for structural stability, in computer science to write code, and in finance to calculate interest and predict trends. Patterns appear throughout nature as well, as the symmetry of a snowflake.
What are the different types of patterns?
The three most common types are shape patterns, letter patterns, and number patterns. We further categorize number patterns into specific types like arithmetic (adding/subtracting), geometric (multiplying/dividing), and Fibonacci (adding the previous two terms to get the next one).
Patterns: Worksheets
Now that we’ve looked into the pattern meaning, different types of patterns, and seen some examples, it’s time for some practice. The free worksheets below come filled with colorful, fun, and engaging pattern exercises of different levels. Make sure to give them a try!






