• Math tutors
• /
• Knowledge Base
• /
• Perfect Squares – Definition, Formula, List, Examples

Perfect Squares – Definition, Formula, List, Examples

Jessica Kaminski

reviewed by Jo-ann Caballes

Updated on October 3, 2024

At Brighterly, we make math fun and straightforward to understand for kids of all ages. 

In this article, we’re explaining perfect squares, which are essential to understanding bigger mathematical theories including the Pythagorean theorem, quadratic equations and geometric sequences. We’ll cover the definition of perfect squares, the formula to work them out and perfect square examples, plus we’ll share practice questions so you can put your knowledge to the test.

What is a perfect square?

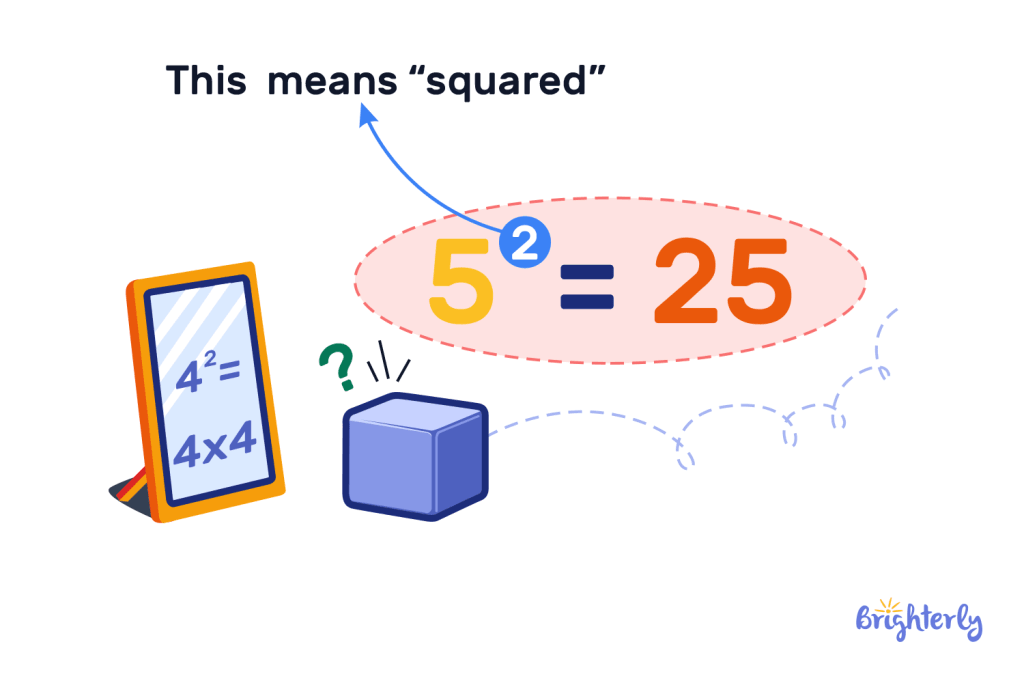
The perfect square meaning is the number you get when you multiply an integer (aka a whole number) by itself. This is also known as squaring a number – so 5 x 5 is also 52 (squared), and the answer is 25. 

A perfect square is not a shape, but it does relate to the shape of a square, which we’ll cover in more detail later on. Here, we’re discussing a numerical square instead of a square shape.

Perfect square definition

The perfect square definition is the result of a number multiplied by itself. The result of any number multiplied by itself is a perfect square, which means that there is an infinite number of perfect squares. 

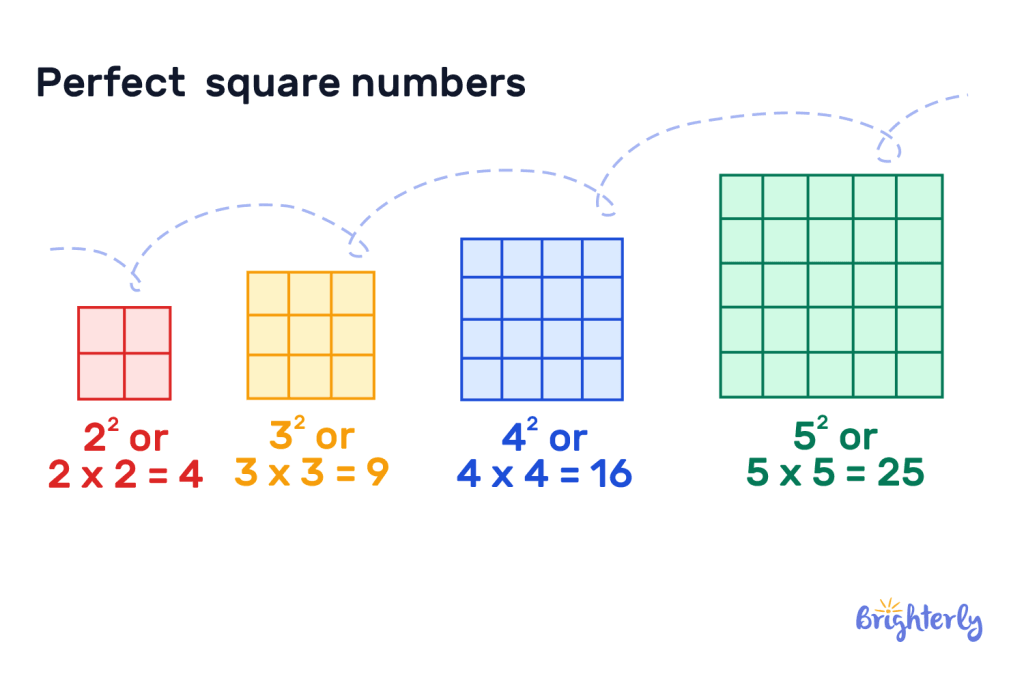
The reason these numbers are called perfect square numbers is because the final number can be arranged to form a perfect square shape made out of smaller squares – find out more about that below.

Perfect squares: examples

There is an infinite number of perfect square examples, so we’ve included the first 20 numbers that are perfect squares here and their perfect square roots:

You’ll see in our graphic below that when each digit of the result is represented by a square, they can all be formed to create an equal-sided square – hence the name perfect squares!

You might also notice a pattern here, in that all of our perfect square numbers above only end in the digits 0, 1, 4, 5, 6 and 9. This is true for all perfect squares, even beyond 400.

Perfect square formula

The perfect square formula is nice and simple. If our final number is ‘n’ and our squared number is ‘x’, the formula is: 

n = x2 

or 

n x n. 

That’s because all you need to do to find a perfect square is multiply an integer by itself.

Perfect squares list

As there are an infinite number of perfect squares is available, we cannot list them all here! Below, we’ve included the first 20 in the list of perfect squares:

• 1
• 4
• 9
• 16
• 25
• 36
• 49
• 64
• 81
• 100
• 121
• 144
• 169
• 196
• 225
• 256
• 289
• 324
• 361
• 400

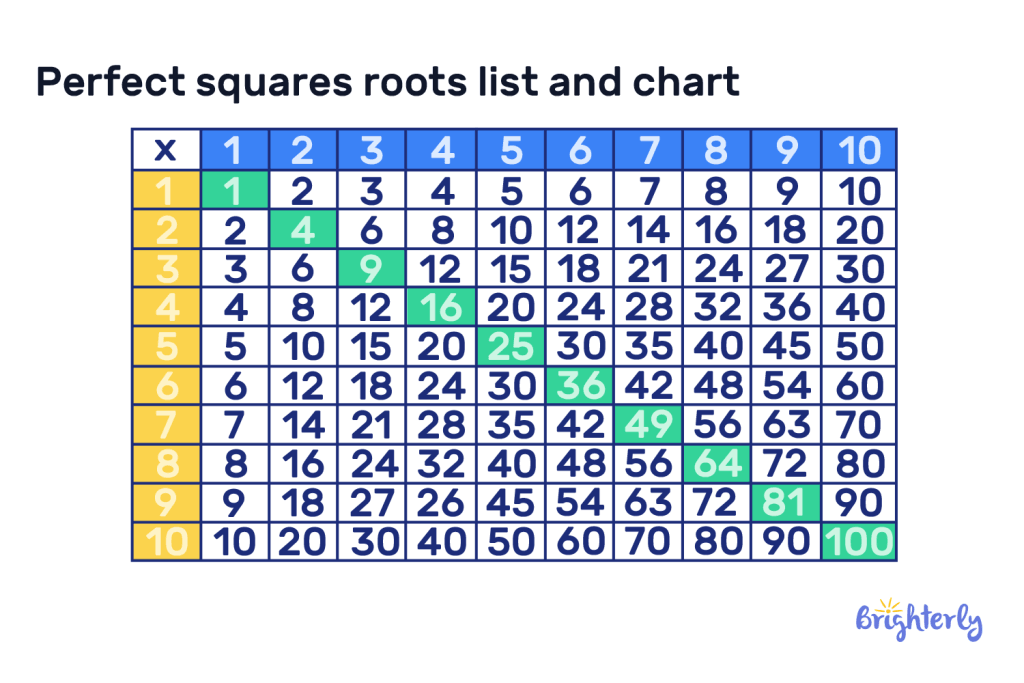
It can also be helpful to visualize your perfect squares list as a chart, like the chart below. This helps kids to visualize the effect of squaring numbers and understand the pattern that emerges with perfect square numbers.

Math tutors

Join Brighterly for personalized lessons for your child

Meet the best tutors for interactive math learning.

Book free lesson

Perfect squares roots list and chart

How to identify perfect squares?

If you want to identify whether a number is a perfect square or not, you need to find its square root. If the square root is an integer (i.e. a whole number), you’ve identified a square number. 

For example, if we take 64, its square root is 8. Because 8 is a whole number, 64 is a perfect square. 66, however, has a square root of 8.12403840464. This number is not an integer, so 66 is not a perfect square.

Identifying a perfect square: key observations

We have some key observations you’ll want to know when identifying a perfect square. It might feel daunting to work out the square root of a number in order to understand if it’s a perfect square, so we have a few neat tricks to make identifying a perfect square easy!

Using perfect square factors

You can work out if a number is a perfect square by using its factors. With any given number, work out all of its integer factors. So if we take 100 as a perfect square example, its factors are:

• 1 (12 = 1)
• 2 (22 = 4)
• 4 (42 = 16)
• 5 (52 = 25)
• 10 (102 = 100)
• 20 (202 = 400)
• 50 (502 = 2500)

Then, you can multiply all those numbers by themselves to see if any result in your number. You’ll see here that 10 x 10 = 100, so 100 is a square number.

If we take 99 as an example, its integer factors are:

• 1 (12 = 1)
• 3 (32 = 9)
• 9 (92 = 81)
• 11 (112 = 121)
• 33 (332 = 1089)

None of those numbers multiplied by themselves result in 99, so we can conclude that 99 is not a perfect square.

Using patterns and rules

We also have another trick up our sleeves using the patterns generated by perfect squares in sequence. It’s a fact that all perfect squares end in one of the following digits: 0, 1, 4, 5, 6, 9. If your number doesn’t end in any of these digits, you can immediately eliminate it knowing it is not a perfect square.

There are some unit place digit rules that you can use to identify perfect squares:

• The perfect square of numbers ending in 3 or 7 have the unit place digit of 9.
• The perfect square of numbers ending in 4 or 6 have the unit place digit of 6.
• The perfect square of numbers ending in 5 have the unit place digit of 5.
• The perfect square of numbers ending in 2 or 8 have the unit place digit of 4.
• The perfect square of numbers ending in 1 or 9 have the unit place digit of 1.

Check out these additional rules for perfect squares too:

• If a number ends in an odd number of 0s, it’s never a perfect square – so 10 and 1,000 aren’t perfect squares (odd number of 0s), but 100 is (even number of 0s).
• Not all numbers ending with an even number of 0s is a perfect square – 100 and 400 are, but 300 is not a perfect square.

All perfect squares are positive

Our final trick is knowing that all numbers that are perfect squares are positive numbers. That’s because a positive multiplied by a positive is a positive and a negative multiplied by a negative is a positive. You cannot make a perfect square by multiplying a positive by a negative because that’s not squaring a number.

Solved math tasks: examples

Which is a perfect square?

Out of these numbers, which is a perfect square?

• 12
• 35
• 52
• 81

Answer:

Find all of the perfect square factors of the above numbers:

• 12: 1, 2, 3, 4, 6
• 35: 1, 5, 7
• 52: 1, 2, 4, 13, 26
• 81: 1, 3, 9, 27, 81

Multiply each of those factors by themselves. The only factor that results in one of your four numbers is 9 into 81, so the answer is 81.

Work out the square root of 64

Work out the square root of 64, then tell us if it is a perfect square.

Answer:

The easiest way to work this out is to list all of the factors of 64, then multiply them by themselves:

• 1 x 1 = 1
• 2 x 2 = 4
• 4 x 4 = 16
• 8 x 8 = 64
• 16 x 16 = 236
• 32 x 32 = 1,024

Here, we can see that 8 x 8 = 64, making it a perfect square.

Find the perfect squares between 30 and 40.

Identify any and all perfect squares between 30 and 40.

Answer:

You can calculate this in a number of ways, from using your perfect squares lists to multiplying numbers from 1 upwards until you get an answer that’s larger than 40. Any number(s) sitting between 30 and 40 will be your answer.

Perfect squares: practice math problems

Perfect squares worksheets

Now that you’ve learnt all about perfect squares, including their definition, formula and how to work them out from your end number, why not put your knowledge to the test with our engaging math worksheets?

• Systems of equations worksheets
• Factor tree worksheets
• Factoring trinomials worksheets
• 6th grade multiplication worksheets

Jessica Kaminski

67 articles

Jessica is a a seasoned math tutor with over a decade of experience in the field. With a BSc and Master’s degree in Mathematics, she enjoys nurturing math geniuses, regardless of their age, grade, and skills. Apart from tutoring, Jessica blogs at Brighterly. She also has experience in child psychology, homeschooling and curriculum consultation for schools and EdTech websites.