Perpendicular Lines – Definition, Symbol, Properties, Examples
reviewed by Jo-ann Caballes
Updated on January 13, 2026
Geometry has many fundamental concepts, and one of them is perpendicular lines.
Understanding what are perpendicular lines is essential for everything, from very basic geometry to more complex areas of geometry and math in general. In this article, we will dive deeper into what these lines are, understand their definition and role, look at some examples and problems, and more. Ready? Let’s start!
What does perpendicular mean?
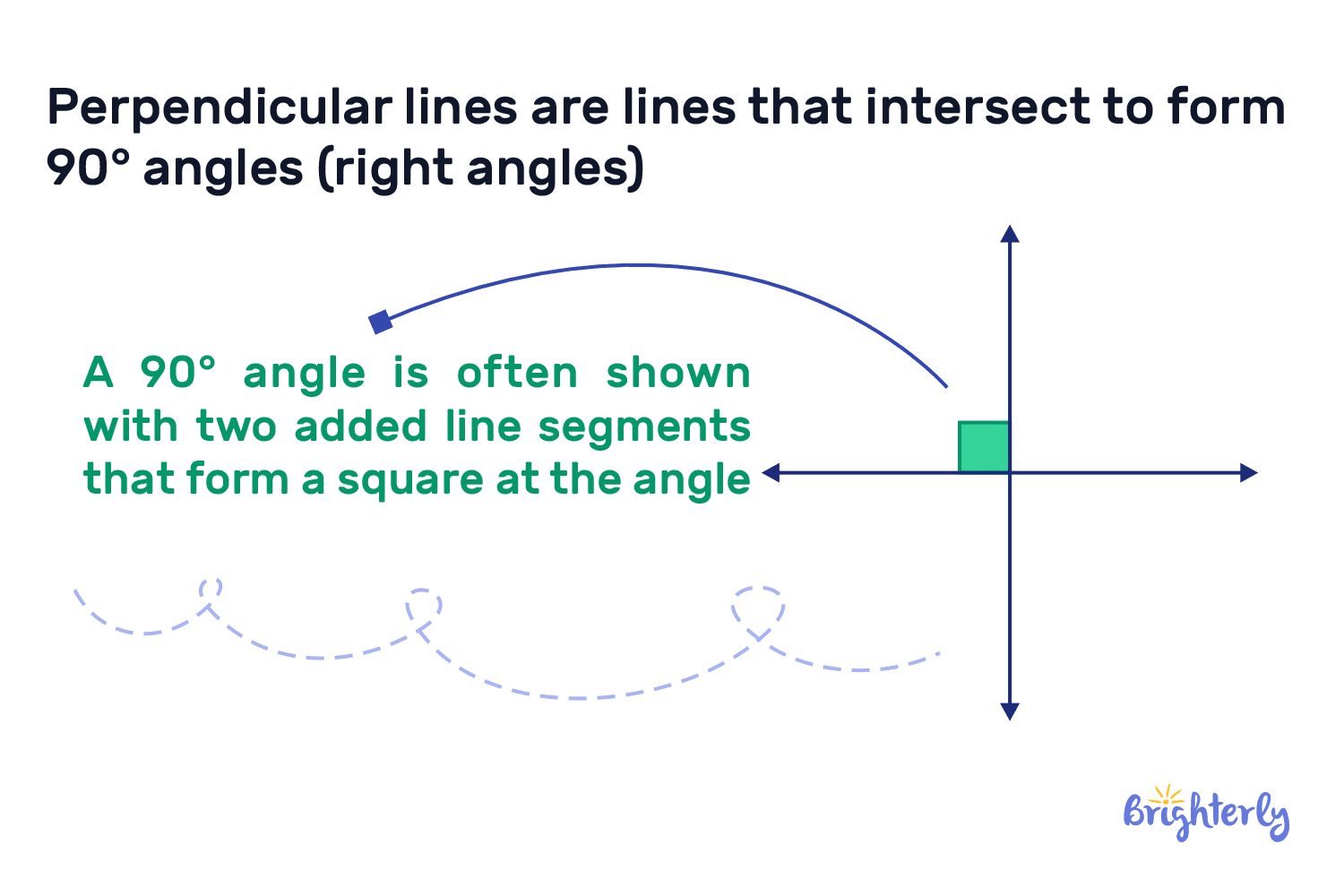
Perpendicular meaning in math refers to lines that intersect and form an angle that is precisely 90° (known as a right angle or perpendicular angle).
In geometry, perpendicularity is almost everywhere. We see perpendicular lines in shapes as common as squares and rectangles (also known as quadrilaterals), which have four right angles. This perpendicularity is also key when we calculate the area and perimeter of these shapes. A right triangle is another of the many shapes with perpendicular sides, where the key to calculating the sides (and essentially, the Pythagorean theorem) is based on the concept of perpendicularity.
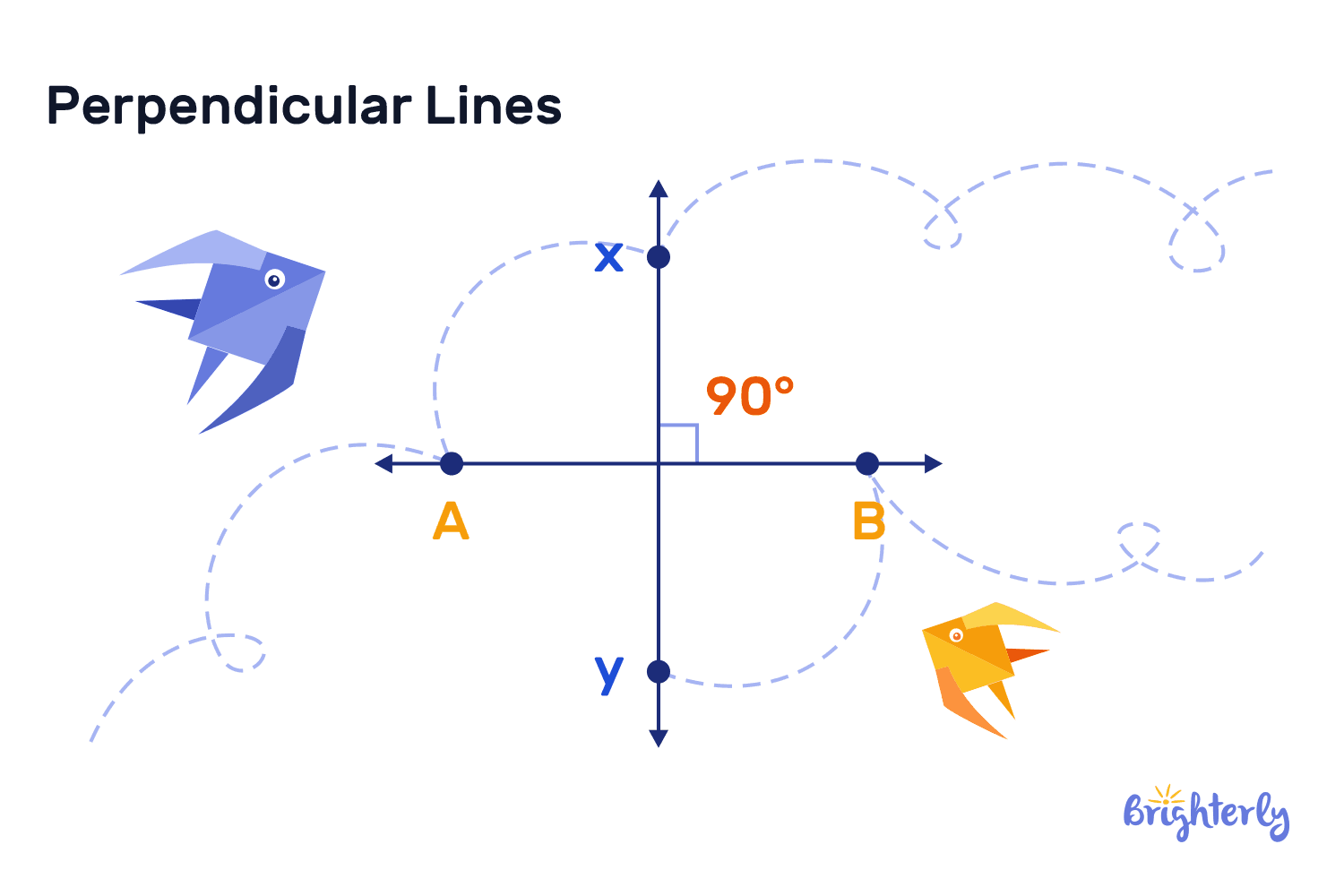
Perpendicular lines definition
Definition of perpendicular lines is, in its simplest form, a very specific rule of intersection. This rule states that perpendicular lines are two lines that meet and cross each other to form an angle of exactly 90°. We also often refer to this angle as the right angle.
When lines are perpendicular (meaning they intersect), they form four right angles and a single point of intersection.
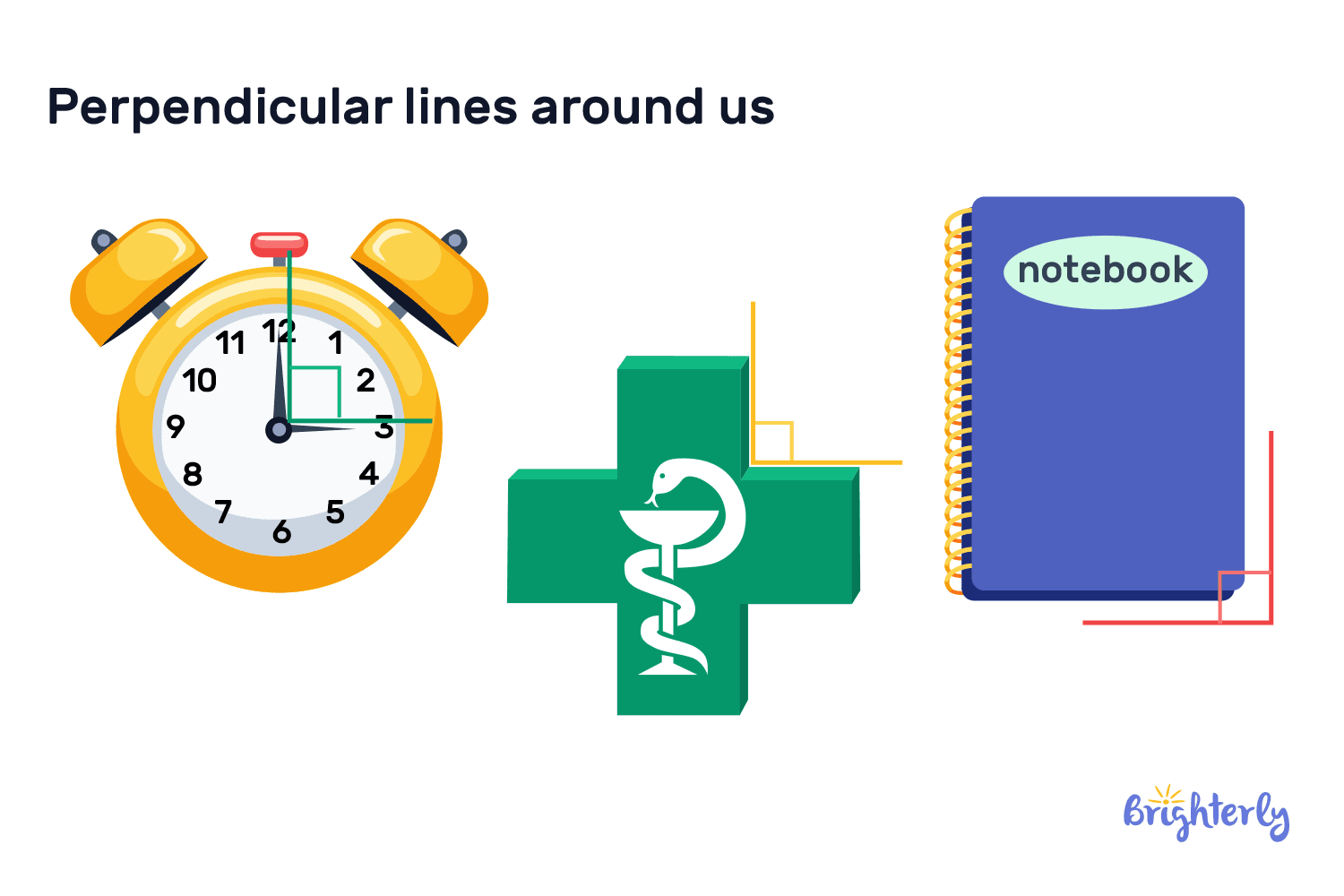
Perpendicular lines examples
In the world that surrounds us, the 90° perpendicular lines have created one of the most common geometric relationships we can find. So, there are plenty of perpendicular lines examples in real life you can find around you, by walking around the street, or even in your home. Some of those are:
- In architecture, including when walls meet the floor and the ceiling, in the frames of windows and doors, and so much more
- In simple objects and signs, like corners of books, the screens of laptops and TVs, writing tables, boxes, tennis courts, and so on
- More abstract, the coordinate system in math uses the x-axis and the y-axis, which are perpendicular lines
There is no shortage of perpendicular line real life example in our surroundings, and it’s because the right angles they form provide us with stability and structure.
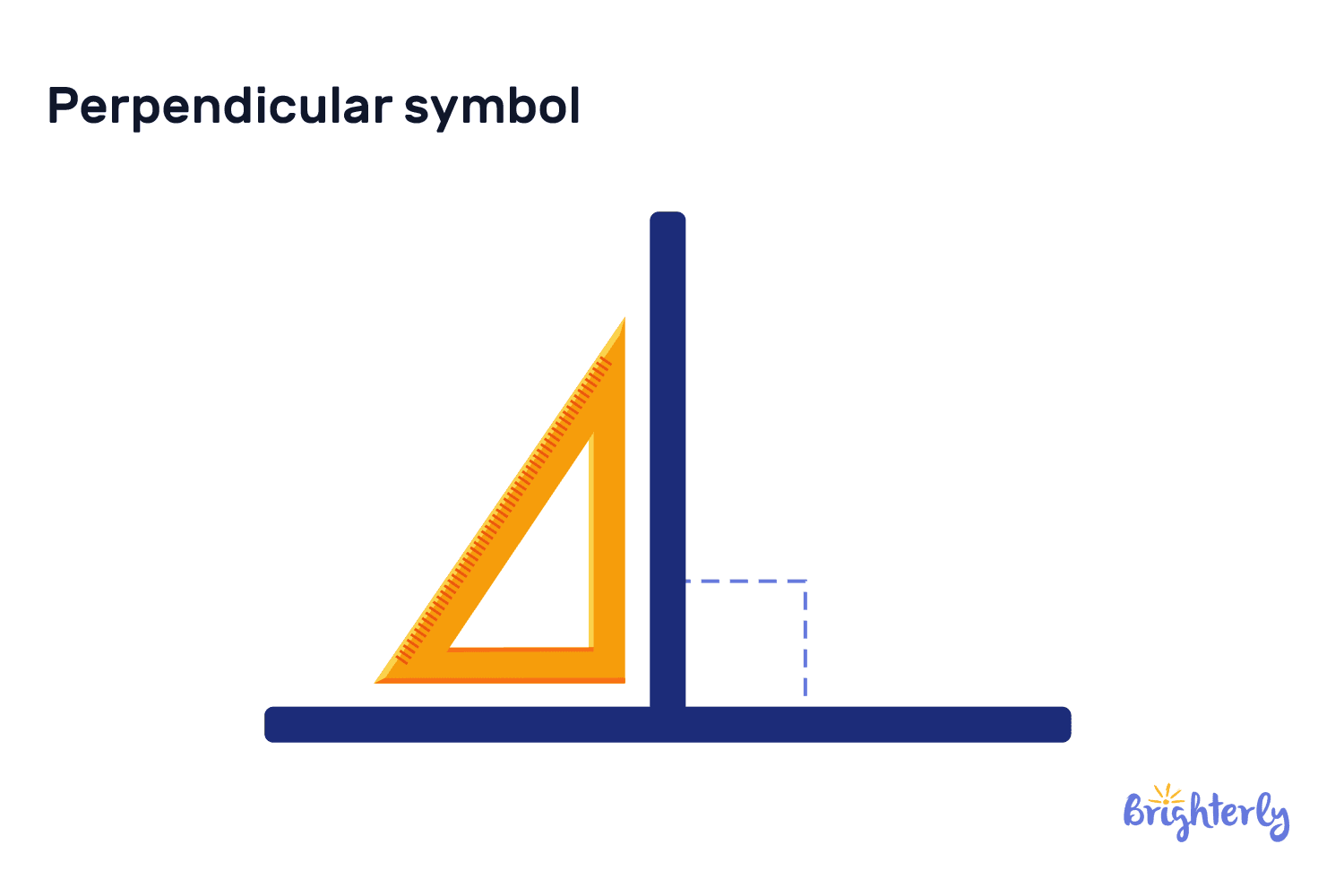
Perpendicular symbol
In the language of mathematics, everything has a symbol, and perpendicular lines are not an exception. The perpendicular sign is a concise, instantly recognizable symbol: this one: ⊥.
As you can see, the symbol for perpendicular lines simply consists of two perpendicular lines forming two right angles. We just like to think of it as an upside-down letter T. Doesn’t get much simpler than that, right?
A standard phrase to use when you want to say that two lines are perpendicular would be AB ⊥ CD. You would read it as “AB is perpendicular to CD”, without having to write that much.
Properties of perpendicular lines
As we define perpendicular lines, it’s also important to mention their properties. These properties are what make perpendicular lines so distinct and crucial in mathematics.
First of those properties is, as discussed earlier, the right angle. It’s also their defining property. Since the intersection is straight, each time the lines intersect, they form four adjacent right angles.
Another one is their relationship to parallel lines. To put it simply, if lines A and B are perpendicular to line C, then lines A and B are parallel and can never intersect.
Perpendicular lines are also unique in the sense that for any given point (both on and off the line), there is only one line that can cross it and be perpendicular. So, for point X, there is only one line A that can intersect with it to form a 90° angle.
And lastly, we also use perpendicular lines to measure the shortest distance. If you want to measure the shortest distance between a straight line and any other point, it would be the line that forms a right angle.
Slope of perpendicular lines
Have you ever noticed that roads or ramps have different degrees of steepness? In math, this steepness is called the slope. And some of the rules governing perpendicular lines are also related to slopes.
When two lines are perpendicular, their steepnesses are interestingly related: they are opposite and reciprocal to one another. So, if line A has a slope m1, line B perpendicular to line A will have a slope m2, which equals to -1/m1. When you multiply these slopes together, you get -1.
This rule does not apply when one line has a slope of 0, because the perpendicular line then has an undefined slope.
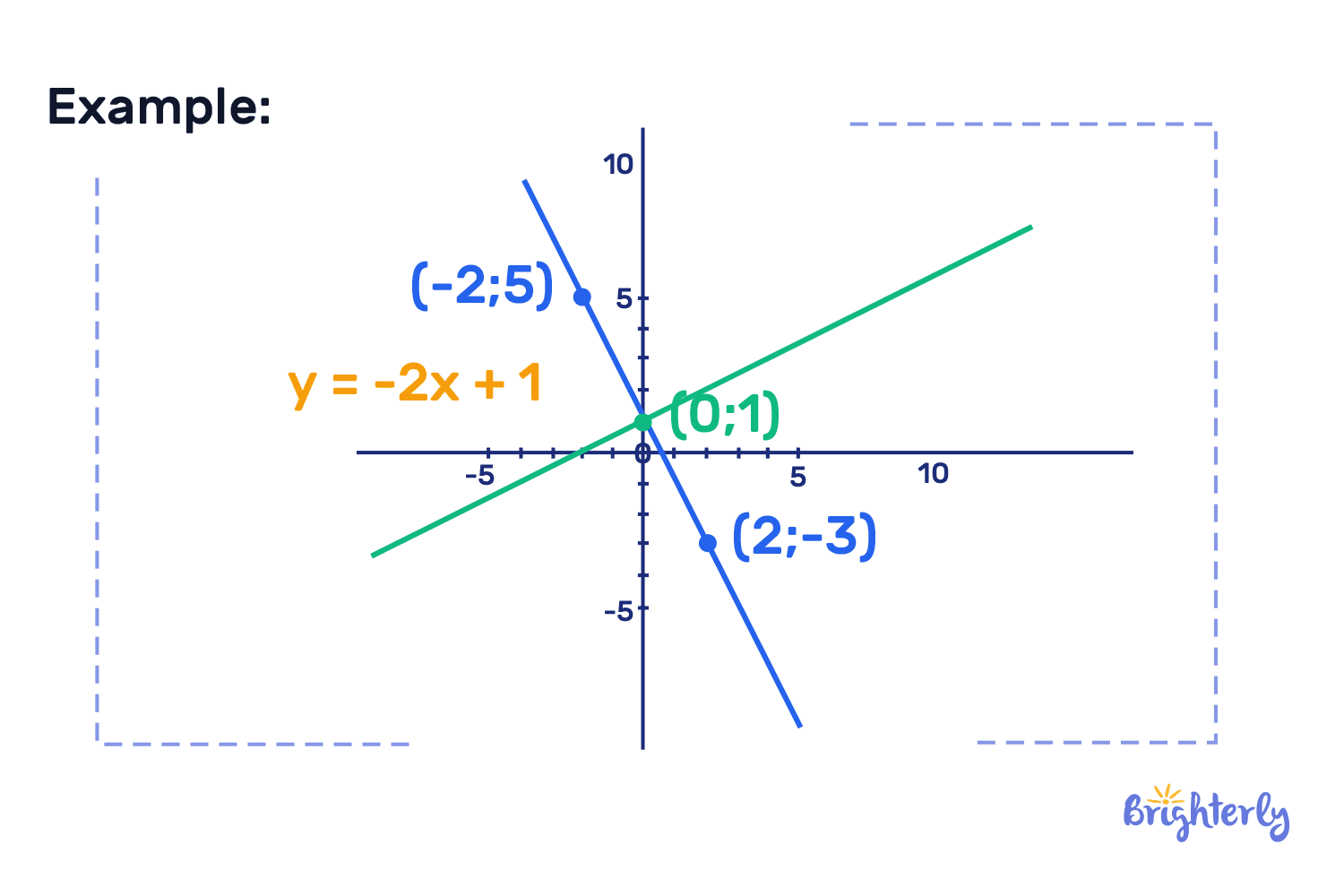
Perpendicular lines and parallel lines: Difference
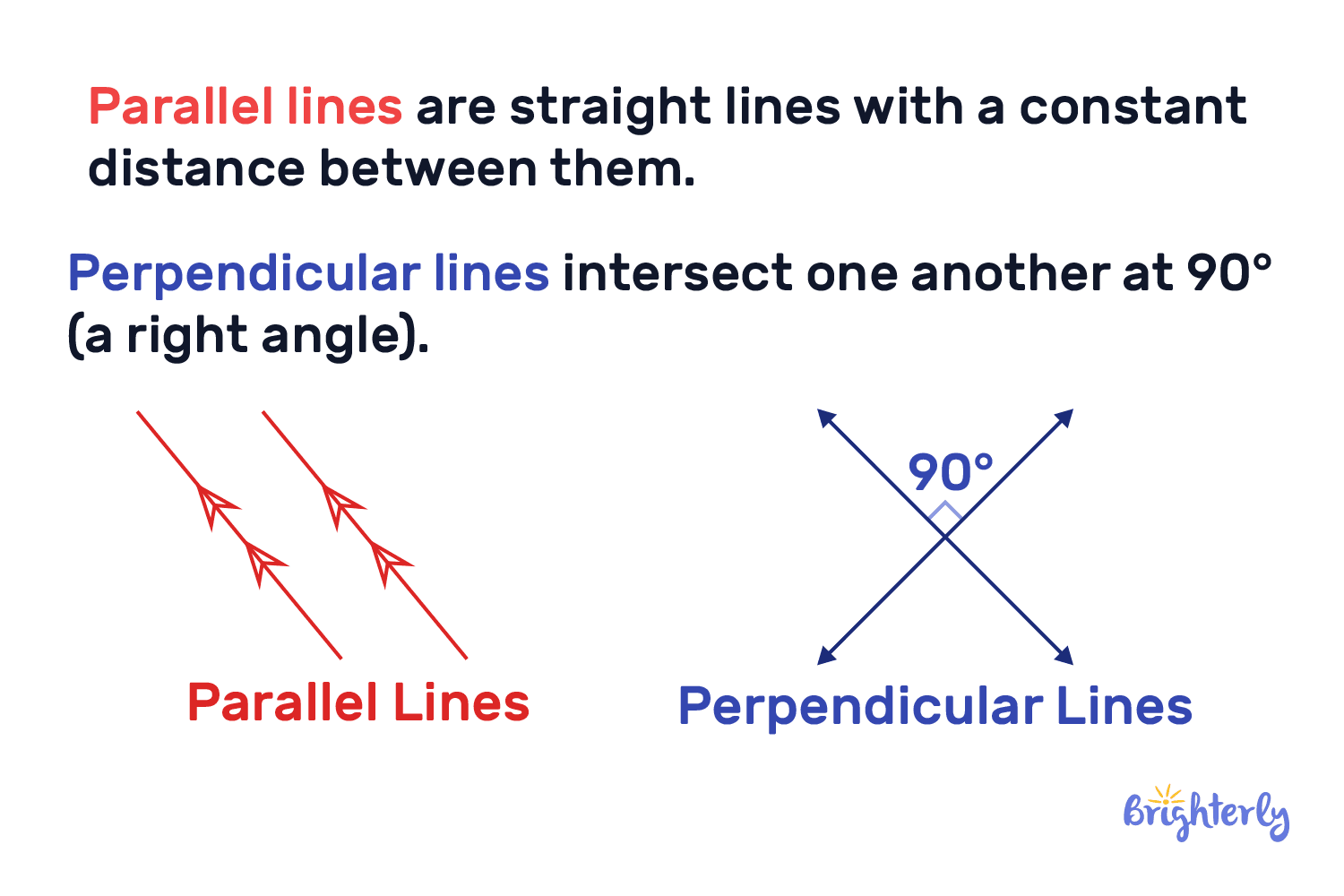
Both of these line types are fascinating mathematical concepts with interesting properties, but at their core, they are fundamentally different concepts.
The core difference is their interaction. We define perpendicular lines by the fact that they must intersect at exactly one location, while parallel lines are defined by the fact that they must never intersect.
These differences in interaction also form the rules that govern these lines. As you already know, perpendicular lines intersect to form a right angle. The lines also have slopes that are negative reciprocals of one another. In contrast, parallel lines run alongside each other, always at the same distance apart and never intersecting, so their slopes are equal. You can see this difference vividly in the image with examples of perpendicular lines and parallel lines below.
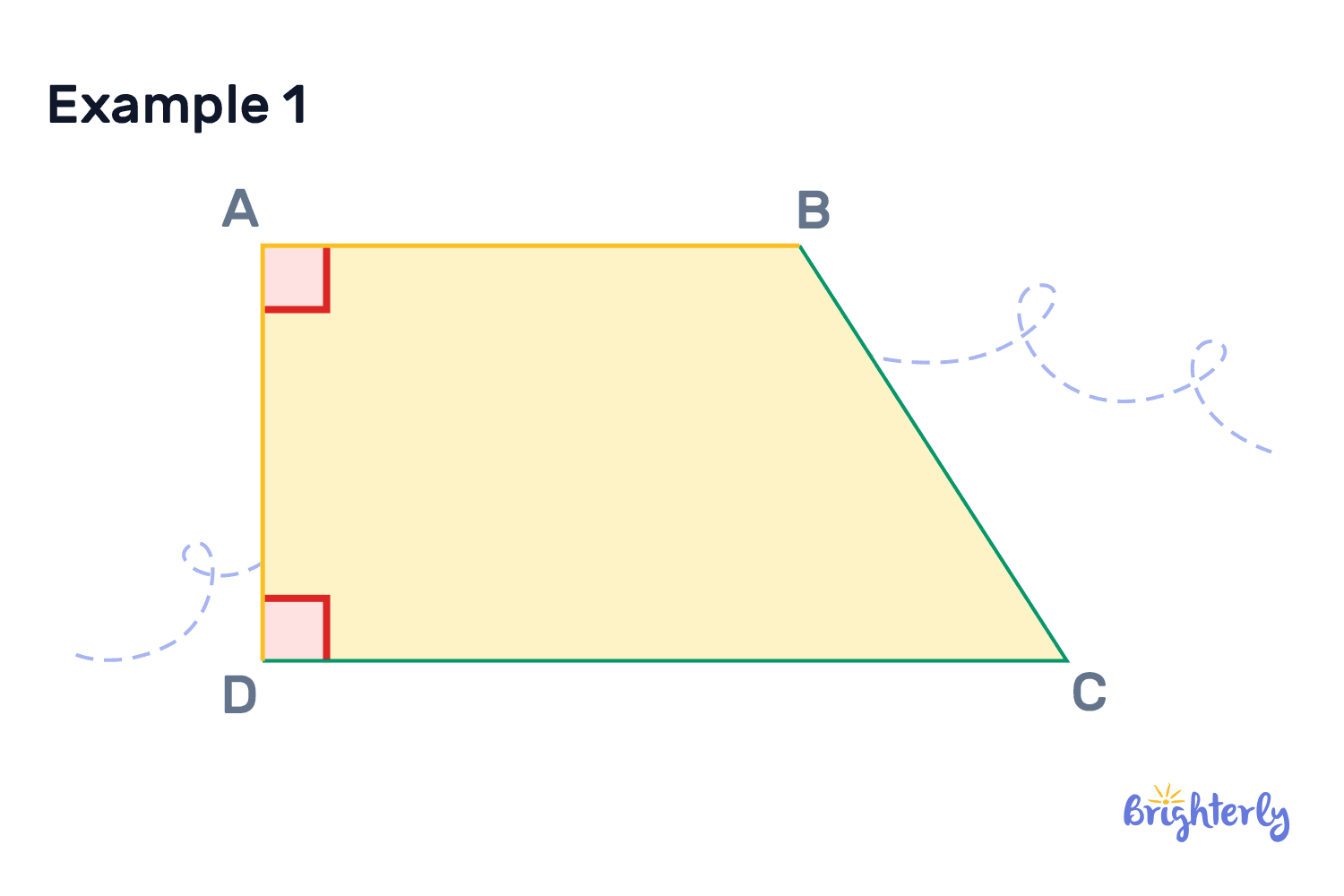
What are perpendicular sides?
Perpendicular meaning in the context of geometric shapes, refers to two adjacent sides of a polygon (a geometrical shape, which we make using three or more straight lines), which form a right angle when they intersect.
Here are some perpendicular shape examples that are more common, and which you have definitely come across:
- Squares and rectangles (both falling under quadrilaterals)
- Right-angled triangles (remember the Pythagorean theorem?)
- Right-angled trapezoids (arguably less common, but you can see this shape in architecture and some everyday objects)
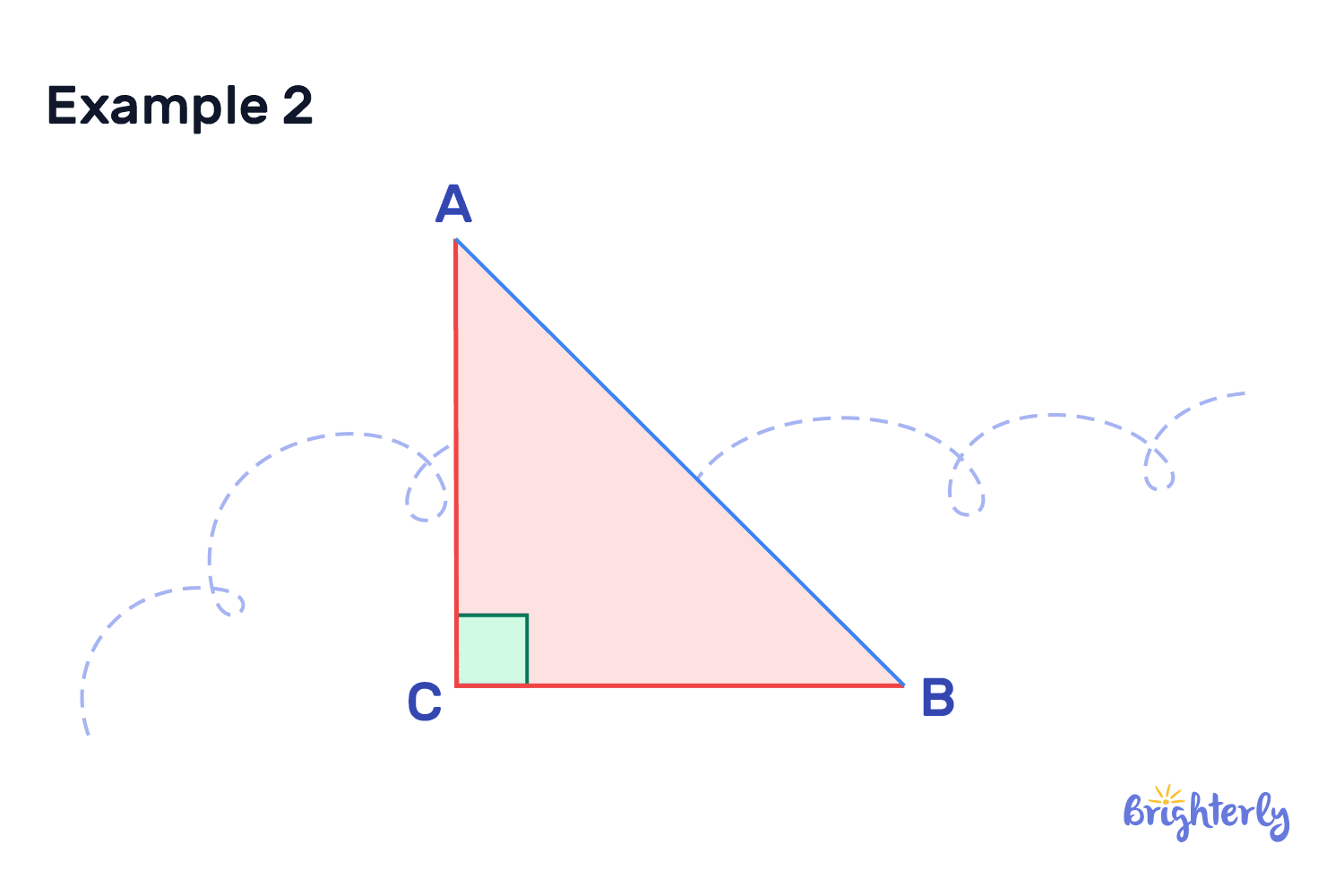
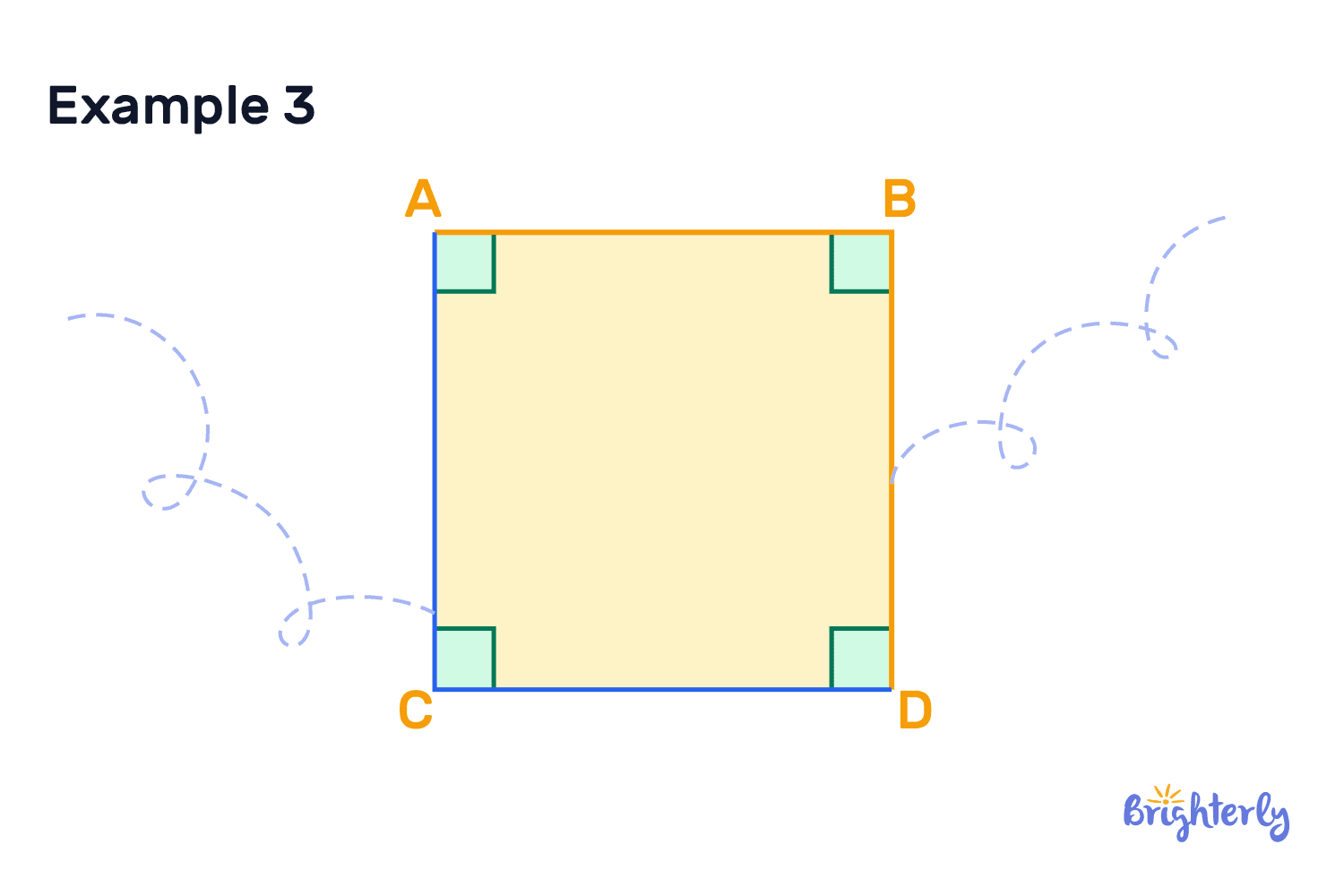
What is a perpendicular angle?
Perpendicular angle is another common term we use to define the precise 90° angle, which two perpendicular lines form at the intersection. If you come across this term, don’t be confused!
Construction of perpendicular lines
There is more than one method for correctly constructing perpendicular lines, but whichever method you choose, the goal will always be to create a perfect 90° angle.
Drawing a perpendicular line using protractor
The simplest and quickest way you can draw perpendicular lines in geometry, relying on direct measurement, is through a protractor. It’s an effective method to go for when very minor imprecisions are fine, and you want to draw the lines quickly.
With this method, you can draw perpendicular lines in a few quick steps. First, draw a straight horizontal line on your paper, parallel to the top and the bottom of your page. Do you know where you want the other line to intersect? Mark that point with a P. Next, place the protractor on that line in such a way that the center falls directly on the marked spot and the baseline of the protractor aligns with your line perfectly. Then, make a small mark on the paper near the 90° on the protractor. Use a ruler to connect your 90° dot to the P. The process will take you less than a couple of minutes!
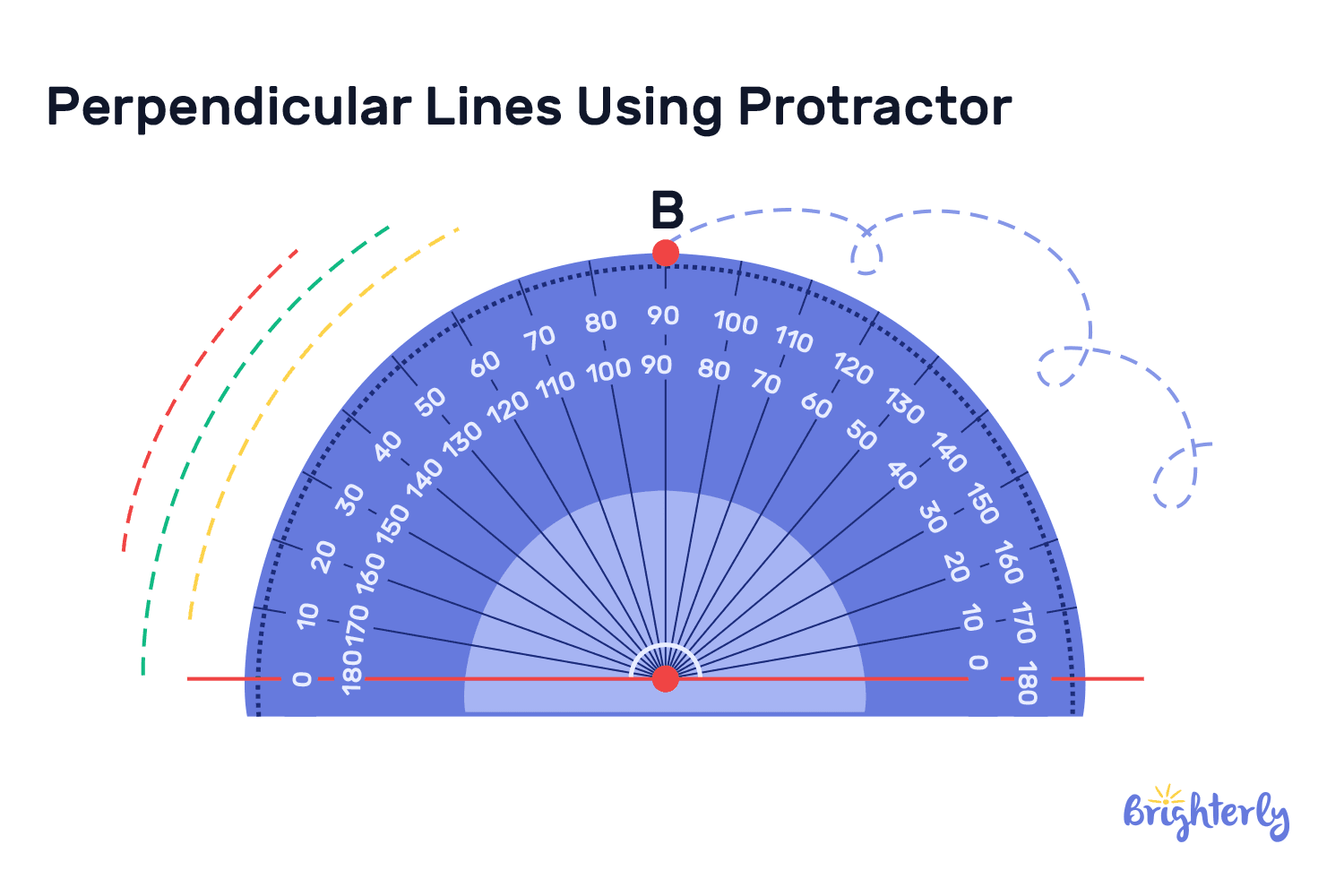
Drawing a perpendicular line at a given point on a line using compass
The next method is another common method to draw perpendicular lines in geometry. It’s less straightforward than the protractor method, but it’s the classic, precision approach. This method is also often called the “constructing” approach, as you need to rely on geometry to construct the lines.
To start, use a ruler to draw a straight horizontal line. Put the needle of your compass on the P you want your lines to interact. Open the compass a little and draw an arc that crosses a baseline on both sides of your P. These two new points are A and B.
Next, open your compass more (wider than the distance between A and P). Put the needle on point A, and draw an arc over the baseline. Then, move the compass to point B, and repeat. The point where both arcs intersect will be our point C. Take a ruler and connect C and P. You now have your perfect perpendicular line!
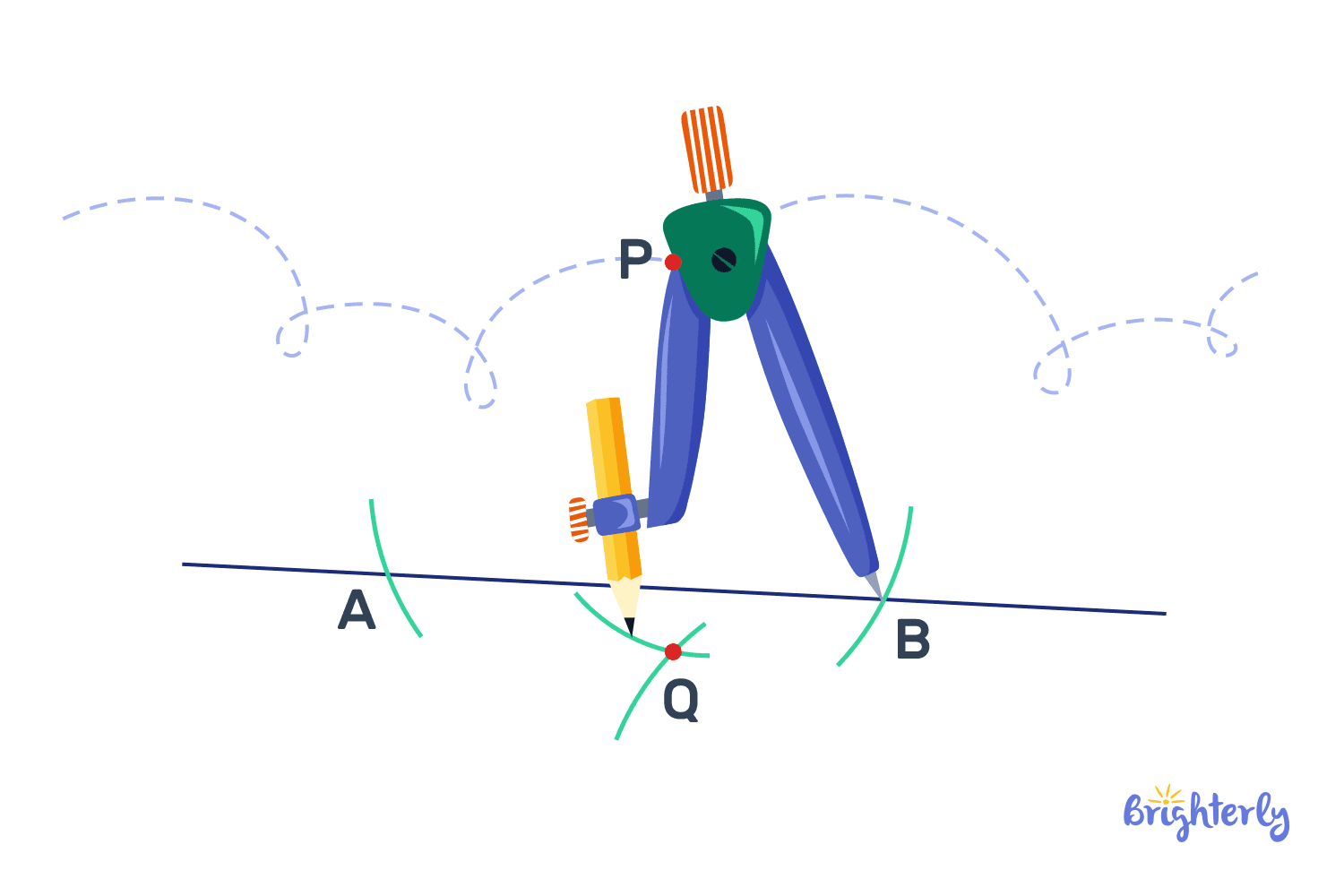
Perpendicular lines in real life
As we mentioned earlier, perpendicular lines are present in real life a lot. In fact, it is one of the most fundamental concepts that governs our world. Every time you see a perfect right angle, you are seeing perpendicular lines in action. The architects and engineers of your home relied on this concept to make sure the structures are sound. From the square tiles of your home to street intersections and everything in between, the perpendicular angle is present wherever we go.
Facts about perpendicular lines
Beyond the right angle and its place in math and the outside world, there are quite a few interesting facts about perpendicular angle and lines.
- The shortest distance from a point to a line is given by the perpendicular from the point to the line.
- For any given point, there is only one perpendicular line possible
- The only exception to the slope rules of perpendicular sides is 0
- If a circle touches a line at point C, and if you draw a radius line from the center of that circle to point C, the lines will always be perpendicular
Perpendicular lines: Solved math tasks
Now that you know everything there is to know about perpendicular lines, including the perpendicular definition geometry, we have included some solved math tasks and perpendicular examples below so you can practice your newfound knowledge.
Solved math task 1
Does this trapezoid shape below have any perpendicular lines or perpendicular sides? Explain why or why not.
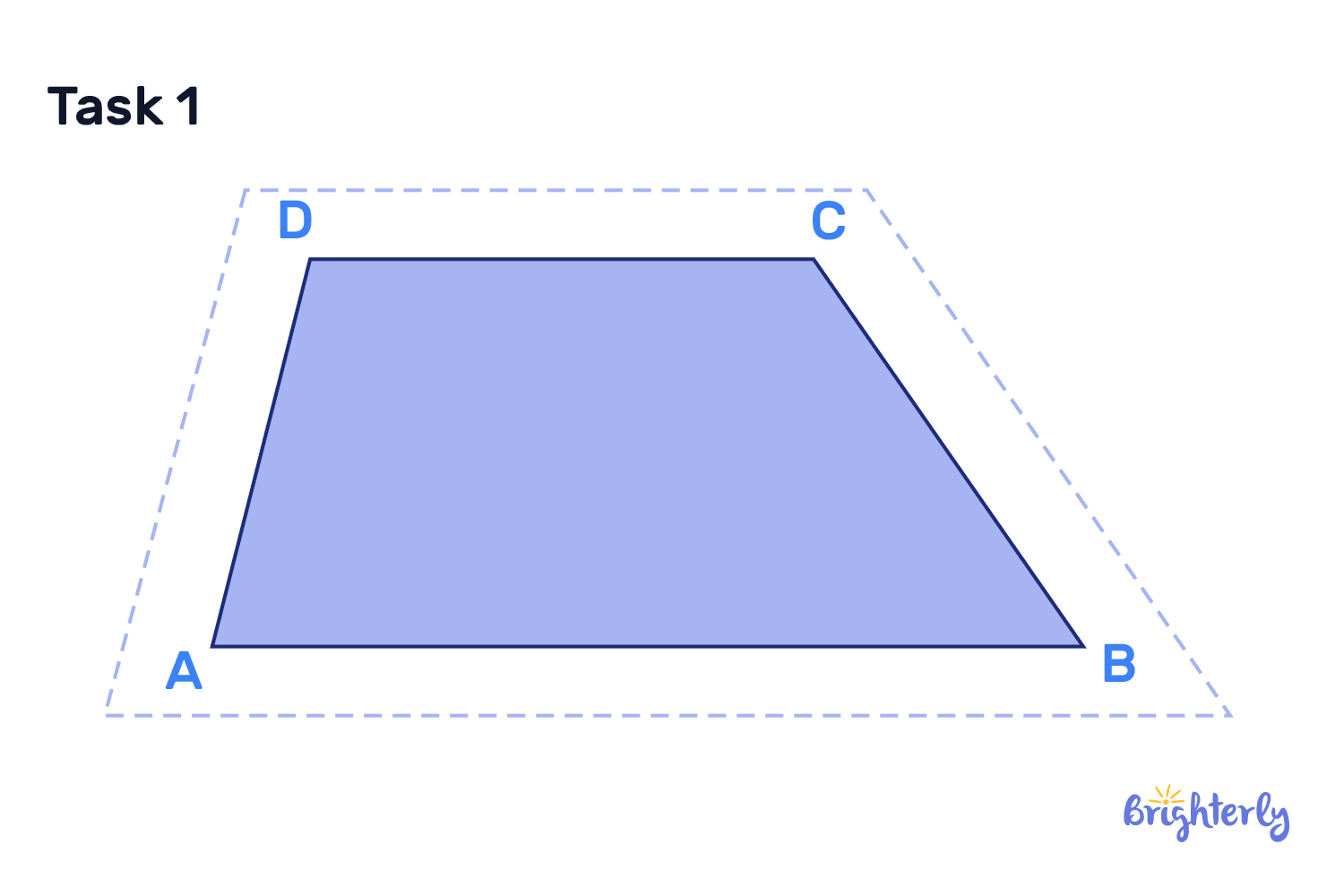
Answer:
| No, the trapezoid does not have any perpendicular lines or perpendicular sides. |
While it has lines and sides that intersect, none of them create a right angle; therefore, they are not perpendicular.
Solved math task 2
Using a ruler, draw a straight line on paper that is parallel to the top and bottom of the paper and is 10 cm long. Draw a point above your line that is exactly halfway along the line.
Using that point, draw a perpendicular line through your original line without using a protractor.
Answer:
| Use the method we detailed earlier on using a compass to draw a perpendicular line using a given point. |
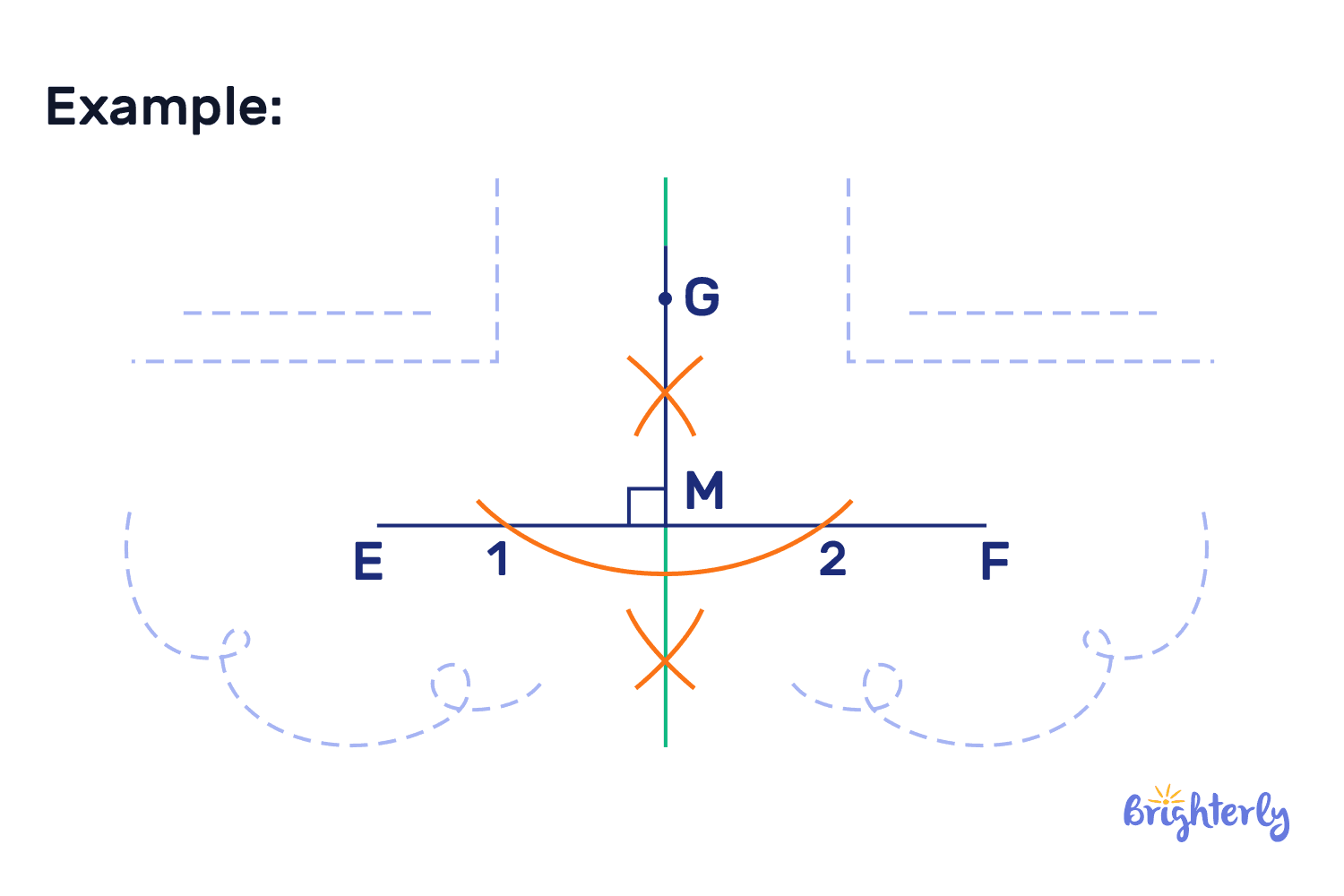
Solved math task 3
Take a look at this diagram. Is OA perpendicular to AB? And what shape will this indicate if you connect the two lines?
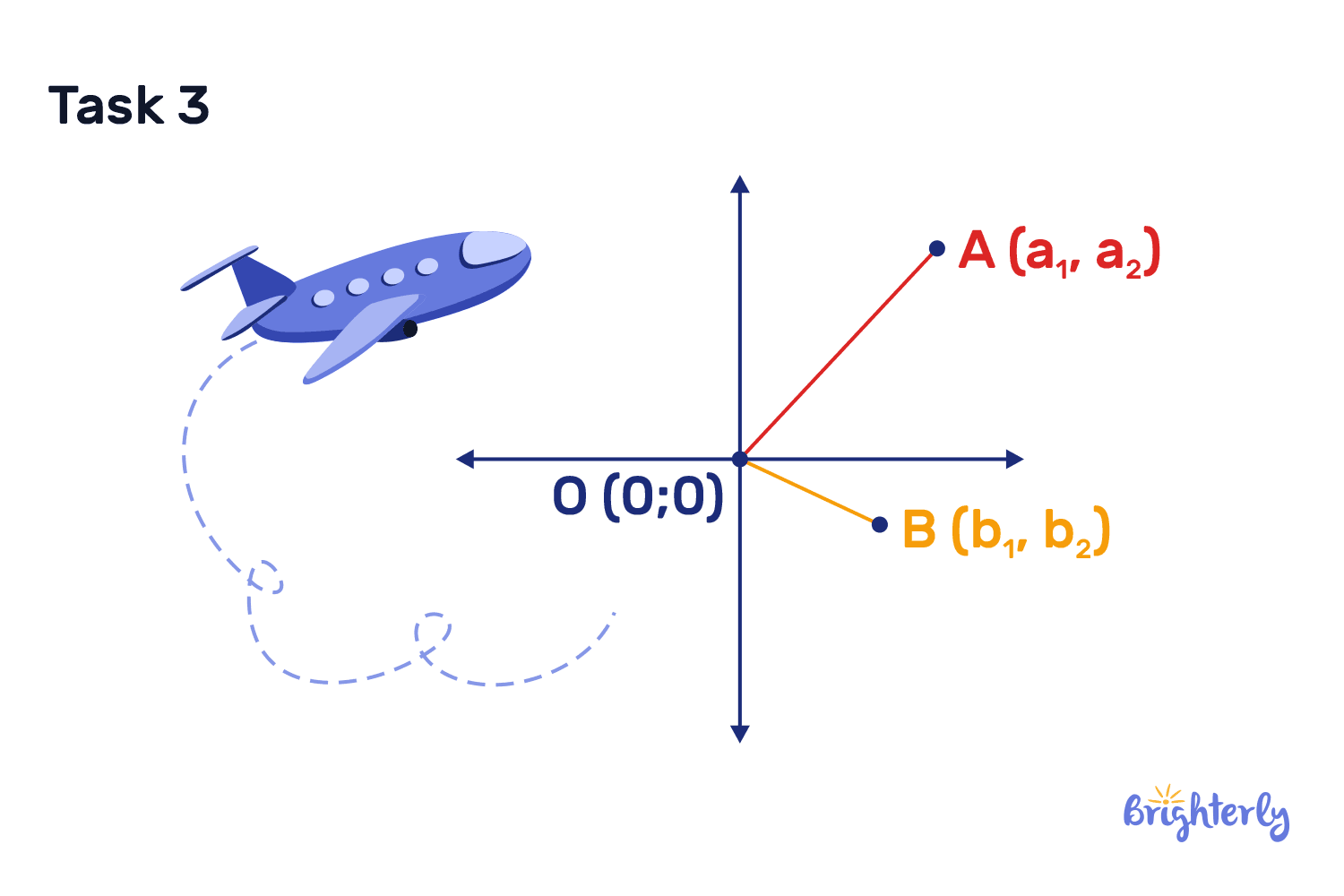
Answer:
| Yes, these lines are perpendicular, because they create a right angle. If we connect both lines, we get a right-angled triangle. |
You can use a protractor to work out the right angle at these perpendicular line intersects, then draw the line from point A to point B to reveal a right-angled triangle.
Perpendicular lines: practice math problems
Frequently asked questions on perpendicular lines
What is a perpendicular line?
Perpendicular lines definition in geometry is that it is a line, ray, or segment of a line that intersects another line or segment at precisely 90°. This intersection forms an angle known as a right angle, which is the defining characteristic of perpendicularity. The perpendicularity is symbolized using ⊥.
What’s the rule for perpendicular lines?
The primary rule of perpendicular sides and shapes is that they must meet to form a right angle. Another rule is that the slopes of the lines are negative reciprocals, which means that when you multiply the slopes of the lines, you need to get -1 as an answer.
What shapes have perpendicular sides?
There are many examples of perpendicular sides in shapes, most well-known of which are rectangles and squares. They have four perpendicular line pairs. Another common example is the right triangle, two sides of which form a 90° angle (hence the name “right triangle”).
How do you know a line is perpendicular?
There are two simple ways to confirm the lines are perpendicular. The first is to measure the angle they form at the intersection is 90°. The other one is to calculate if the slopes of the lines are negative reciprocal (slope A x slope B should be -1).
Do perpendicular lines intersect?
Yes, perpendicular lines must intersect, as their main defining factor is that they form right angles at the intersection. If the lines don’t intersect, they cannot be perpendicular by definition. They shouldn’t be confused with parallel lines, which indeed don’t intersect.
Perpendicular lines worksheets
Now you hopefully know what is perpendicular angle and line are, and how they are fundamental both for geometry and the world around us. Understanding this concept, as well as the idea behind the right angle, is critical for geometry and for appreciating the structures we are surrounded by.
If you want to put your knowledge to the test, make sure to check out the free worksheets we created: