What is radius of a circle? Definition, Formula, and Examples
reviewed by Jo-ann Caballes
Updated on January 13, 2026
A circle is one of the most important shapes in geometry, and one your child will work with a lot. Therefore, it’s important they understand what a circle is and how it functions.
In this article, we will dive deep into one aspect of a circle, its radius. We’ll go over the radius definition in geometry, learn the formula for the radius of a circle and how to find it, look at examples and exercises, and more.
What is a radius?
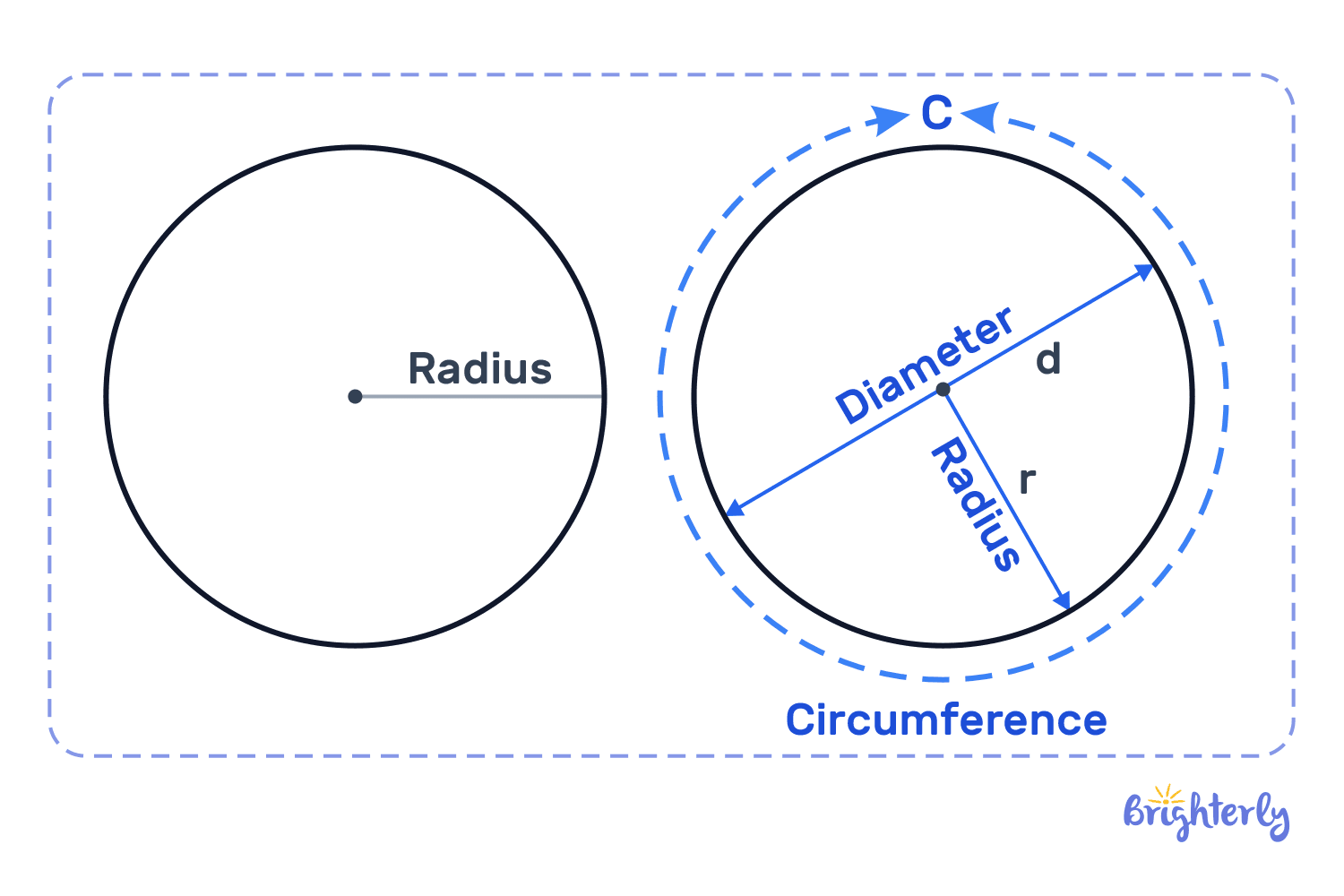
The most basic definition of the radius of a circle is the length of the line you draw from the central point of a circle towards any point of the outer boundary, which in geometry is called the circumference.
Radius is probably the most important feature of a circle, as it defines its size, area, and circumference. Every radius of a given circle will always have the same length.
Radius definition in geometry
The formal radius geometry definition is the distance from the center of the circle to its perimeter.
The radius of circle starts from exactly its center, and shouldn’t be confused with the diameter, which equals the length of two radii and “splits” the circle in half.
Radius examples
The examples of a radius in real life are all around us. In fact, if you look around you now, you will probably see at least one item that has a radius.
This is because a circle is such a fundamental shape common in the world we live in. Some common radius real world example items are:
- Analog clocks, the hands of which are the radius of the circular path they take
- Bicycle wheels, each metal spokes represents a radius
- Pizza slices, when cut from the center, are another circle radius example you’ve definitely come across
From cups and plates to steering wheels, radius is everywhere.
What is the radius of a circle?
Radius in a circle is the distance from the edge of the circle to its very center. Radius will be the same no matter which part of the edge you connect to the center.
Radius of a circle example
You can find other examples of a circle radius all around you, including
- Cakes
- Balls
- A slice of an orange
- The Moon
- Basketball hoop
All of these circular objects have a radius and a diameter.
Radius of a circle formula
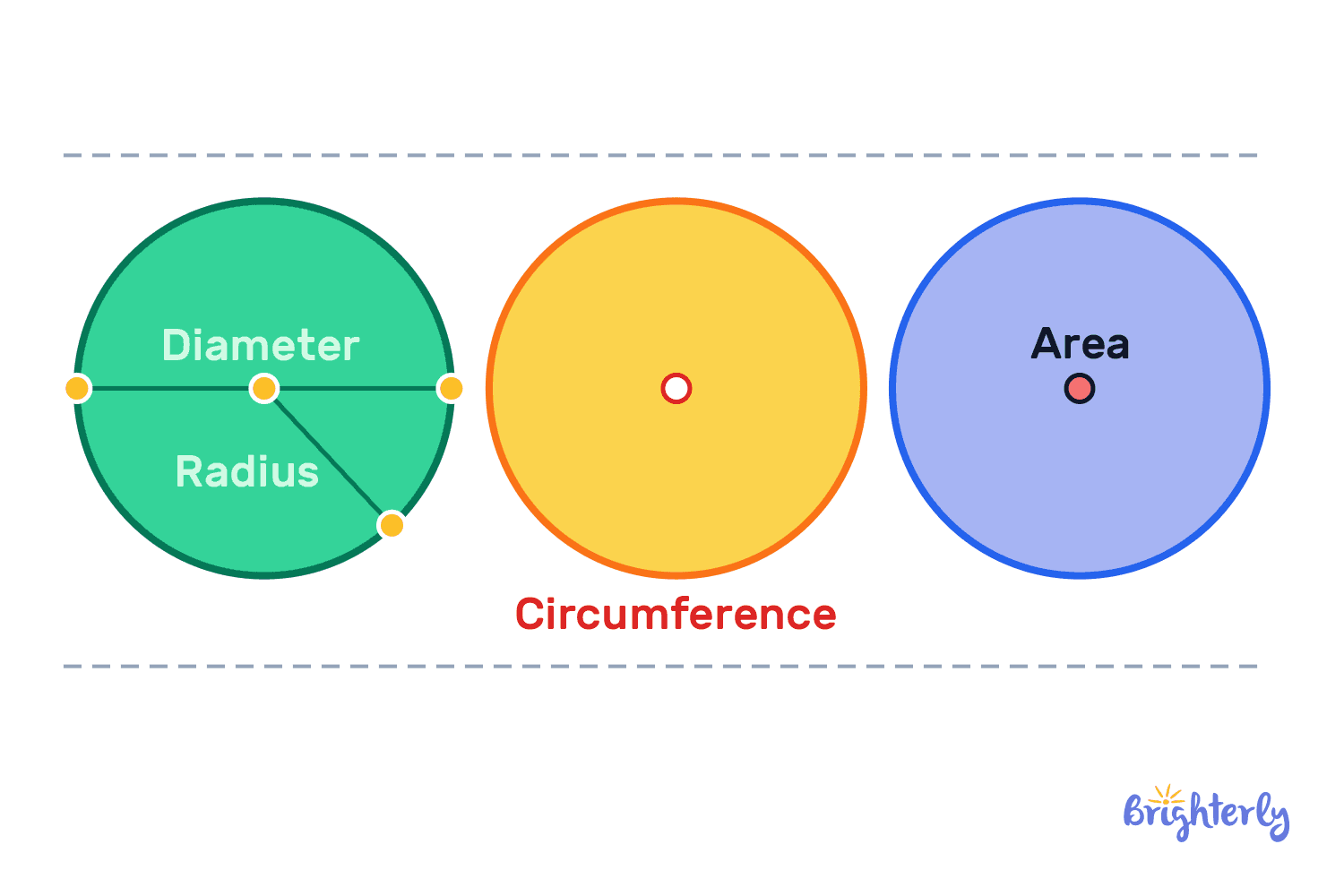
As a geometrical shape, neither the circle nor its radius is random. In fact, they have formulas your kid can use to calculate the radius of a given circle using the circle area and the diameter. The formula your kid needs to use when calculating the radius depends on the information they already have.
In this section, we will look into the three most common ways to find a radius in circle, which are the diameter, circumference, and area.
Radius of a circle formula with area
The area of a circle is the space it occupies. If your kid knows the area of a circle, they can use that information to calculate the radius of the circle.
A = π × r2
Where A is the area, and r is the radius. π (reads as pi) is a mathematical constant, and is approximately equal to 3.14159. The number π is the ratio of the circumference to its diameter.
To calculate the radius, students need to divide A/π, then find the square root of that number. So, the formula to find the circle radius is:
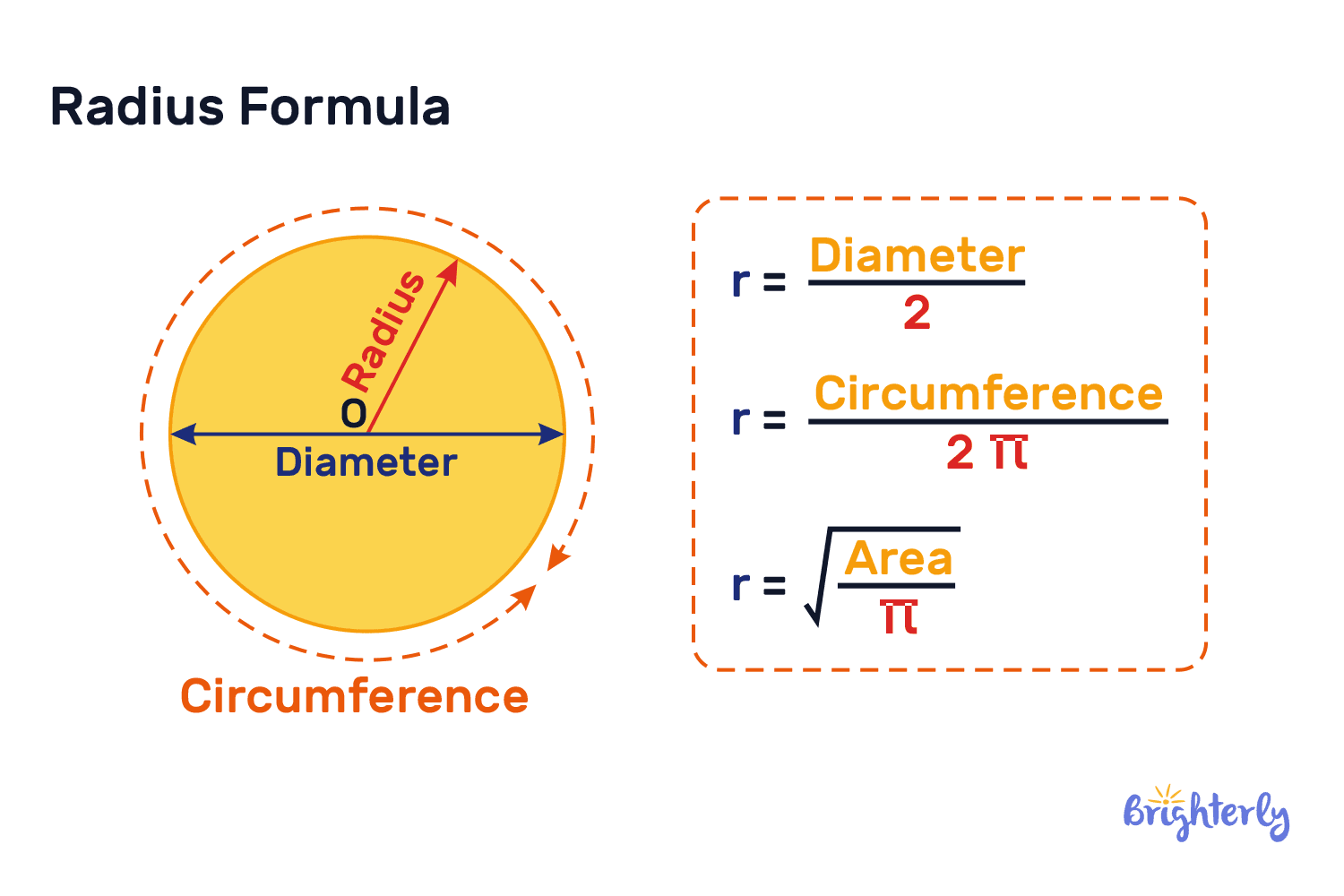
Radius = √Area/ π
Formula for radius of a circle using the diameter
Next up is the radius of circle formula using the diameter. This one is quite simple, really. We mentioned earlier that radius shouldn’t be confused with the diameter.
Diameter is the length from one end of the circle to another, which passes through the center of the circle. It’s the longest line in the circle. The diameter of a circle is twice the size of the radius. And since diameter = radius x 2, the formula to find the radius when the diameter is known is
Radius = diameter / 2
Formula for radius using the circumference
Lastly, let’s look at how your kid can find the radius if they know the circle’s circumference.
As you may remember, the circumference is the total distance around the edge of the circle. If you draw a circle, imagine the circumference as the length of the line you drew. Since diameter = radius x 2, circumference can be expressed in two ways:
- Circumference = π × d
- Circumference = π × 2r
If you know how long the circumference is, you can calculate the radius using this formula:
R = C/2π
Radius of a circle equation
Another formula we want to look at is one that helps you calculate the radius using only the radius coordinates and a point on the circumference. This equation may look a bit more confusing than the ones before:
(x − h)2 + (y − k)2 =r2
r = radius
h, k = coordinates of the center of the circle
x, y = point on the edge of the circle
Once you put in the values and make the calculations, you can get your radius by taking the square root of the number on the right side of the brackets. For example, if r2 = 25, r = 5.
How to find the radius of a circle: Solved math tasks
1. Find the diameter of the circle with radius of 7cm.
Solution: Use the formula radius = diameter / 2, so use the formula diameter = radius x 2
Answer:
| Diameter is 14 |
2. What is the radius of a circle if the area is 78.5 cm²?
Solution: The formula is radius = √Area/ π = √78.5/3.14 ≈ √25 ≈ 5
Answer:
| Radius is 5 |
3. The circle has a circumference of 12.56. What is the radius?
Solution: The formula you need to use is Radius = Circumference/2π. When calculating, R = 12.56/(2×3.14) ≈12.56 / 6.28 = 2
Answer:
| Radius is 2 |
The radius of a circle: Practice Math Problems
Frequently asked questions on radius of a circle
What is a radius of a circle?
The radius of a circle definition is that it’s the length of the straight line that connects the center of the circle to any point on its circumference (which is the outer line of the circle). In exercises and formulas, we typically use the letter r to denote radius.
Is radius half of diameter?
Yes, the radius is half of the diameter. By definition, a diameter is the line that connects two points on the circumference of the circle while going through the circle’s center. The diameter is the longest line possible inside the circle.
How do you find the radius of a circle?
Depending on the information you have, there are several methods to find the radius of a circle. If you know the diameter, you can divide it by 2 to get the radius. If you know the circumference, you can divide it by 2π to find the radius.
Is radius the same as circumference?
No, radius and circumference are completely different concepts in a circle. Circumference is the total distance outside of the circle, its perimeter, while radius is a straight line connecting any point of the circumference to the center of the circle. Radius is the same for all points on the circumference.
How to find radius with circumference?
If you know the circumference of the circle, you can find the radius with this easy formula: r = C/2π, where C = circumference. For example, if C = 18.72, r = 18.72/(2×3.14) = 3.
The radius of a circle: Worksheets
Understanding the radius is the first step children can take towards unlocking the geometry of a circle. Whether your child needs to calculate the area inside a circle or the circumference, knowing or being able to find the radius is an essential starting point.
Help your child on their way to becoming a geometry pro through these free worksheets, which cover related topics and come filled with engaging and fun exercises that are challenging enough to keep your child interested.
Winter Math & Reading Camp for Grades 1-9
Join Brighterly's Online Winter Camp to excel in math and reading.
Choose kid's grade
Winter Math & Reading Camp for Grades 1-9
Join our Winter Camp, boost your child's math and reading skills.
