Reciprocal: Definition, Math Problems, Solved Math Tasks
reviewed by Jo-ann Caballes
Updated on January 13, 2026
Welcome to another Brighterly knowledge base article, where we try to break down essential math topics and concepts so that they are easy to understand. Here, we are going to look at the reciprocal of a number, a topic that is fundamental to many later math concepts.
We will look into what is a reciprocal, how you can find a reciprocal of a number, as well as explain reciprocals of fractions and reciprocals of negative numbers. Ready? Let’s dive in!
What is a reciprocal in math?
Let’s start with what does reciprocal mean in math. We like to think of reciprocal as the “perfect partner” of each number. Here, by perfect, we mean a number that, when you multiply it by the first number and always gives 1 as the answer. That number is the meaning of reciprocal in math.
Definition of reciprocal in math
The simplest definition of a reciprocal in math is that it is the inverse of a given number. In other words, it’s 1 divided by the number. It works the other way around, too: reciprocal is the number, which, when multiplied by the original number you had, gives you 1 as the answer. So, the reciprocal of a number n is always 1/n.
Here are a couple of examples:
- The reciprocal of 6 is 1/6
- The reciprocal of 20 is 1/20th
Another definition of a reciprocal, which initially may seem a bit more complicated, is a number to the power of -1.
- Reciprocal of 6 is 6-1
- Reciprocal of 20 is 20-1
This is a different notation, but the value of the reciprocal doesn’t change.
How do you find the reciprocal of a number?
Finding the reciprocal of a number depends on whether you are working with whole numbers, negative numbers, or fractions. In this section, we’ll concentrate on finding the math reciprocal of whole numbers.
Here, the process is quite simple: if you remember the trick that every whole number can be represented as a fraction. Then, you can use the turn-and-flip trick to find the reciprocal in two easy steps.
- First, turn the number into a fraction. For this, you simply need to divide your number by 1.
- And then, in the second step, you simply flip the fraction you have and get your reciprocal.
What is a reciprocal of 5?
Now, let’s use these steps and find the reciprocal of 5.
- Turn 5 into a fraction: 5/1.
- Flip 5/1 to get your reciprocal: 1/5.
You can also check if it’s correct by multiplying the original number by the reciprocal. If you get 1 (and 5/1 x 1/5 is indeed 1), then you got it right.
What is the reciprocal of 4/7?
The next reciprocal example is 4/7. As you can see, it’s different because it’s already a fraction. In this case, it simplifies the process even further, as you only need to take one step: flipping the fraction. So, for the original fraction 4/7, the reciprocal is 7/4.
Reciprocal of a fraction
Now, we will have a look at reciprocals of a fraction, and it’s quite exciting, because this is where you can see and understand the reciprocal meaning and concept better.
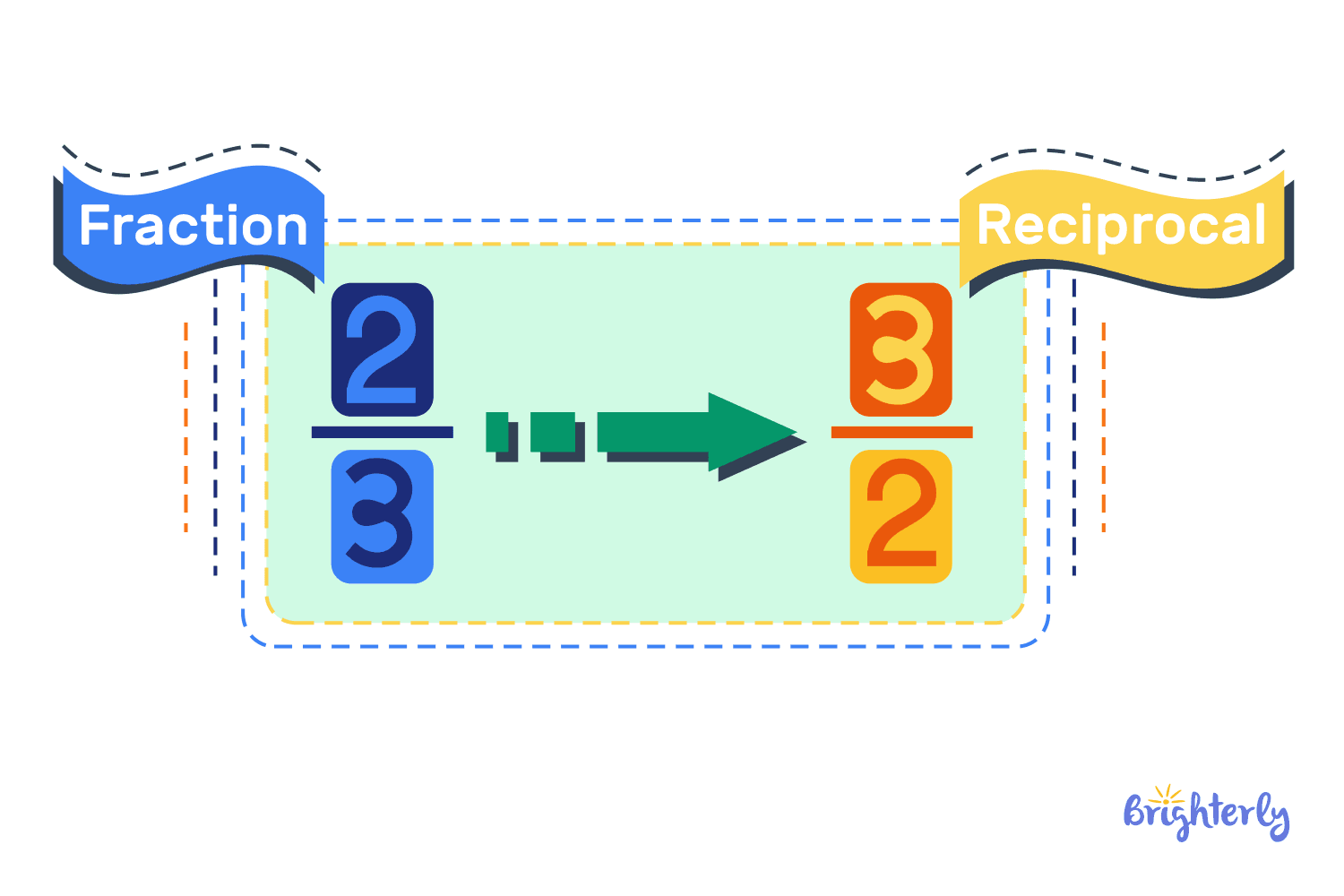
What does reciprocal mean in fractions?
While reciprocal in fractions may sound complicated, in reality, it’s very simple. The reciprocal math definition of a fraction is to simply flip the positions of the numerator and denominator. Let’s look at a couple of reciprocal examples.
You have the fraction 5/6.
- 5 is your numerator (top number)
- 6 is your denominator (bottom number)
When you flip 5/6, the numerator becomes 6, and the denominator becomes 5, and you get your fraction reciprocal 6/5.
Let’s check the math too:
5/6 x 6/5 = (5×6)/(6 x 5) = 1
Another example is 13/16 (original fraction) = 16/13 (reciprocal fraction)
How to find the reciprocal of a fraction?
All you need to do to find the reciprocal of a fraction is to simply flip the fraction, switching the positions of the numerator and denominator. The bottom number goes on top, the top number goes down, and you have the reciprocal of a fraction.
Reciprocals of negative numbers
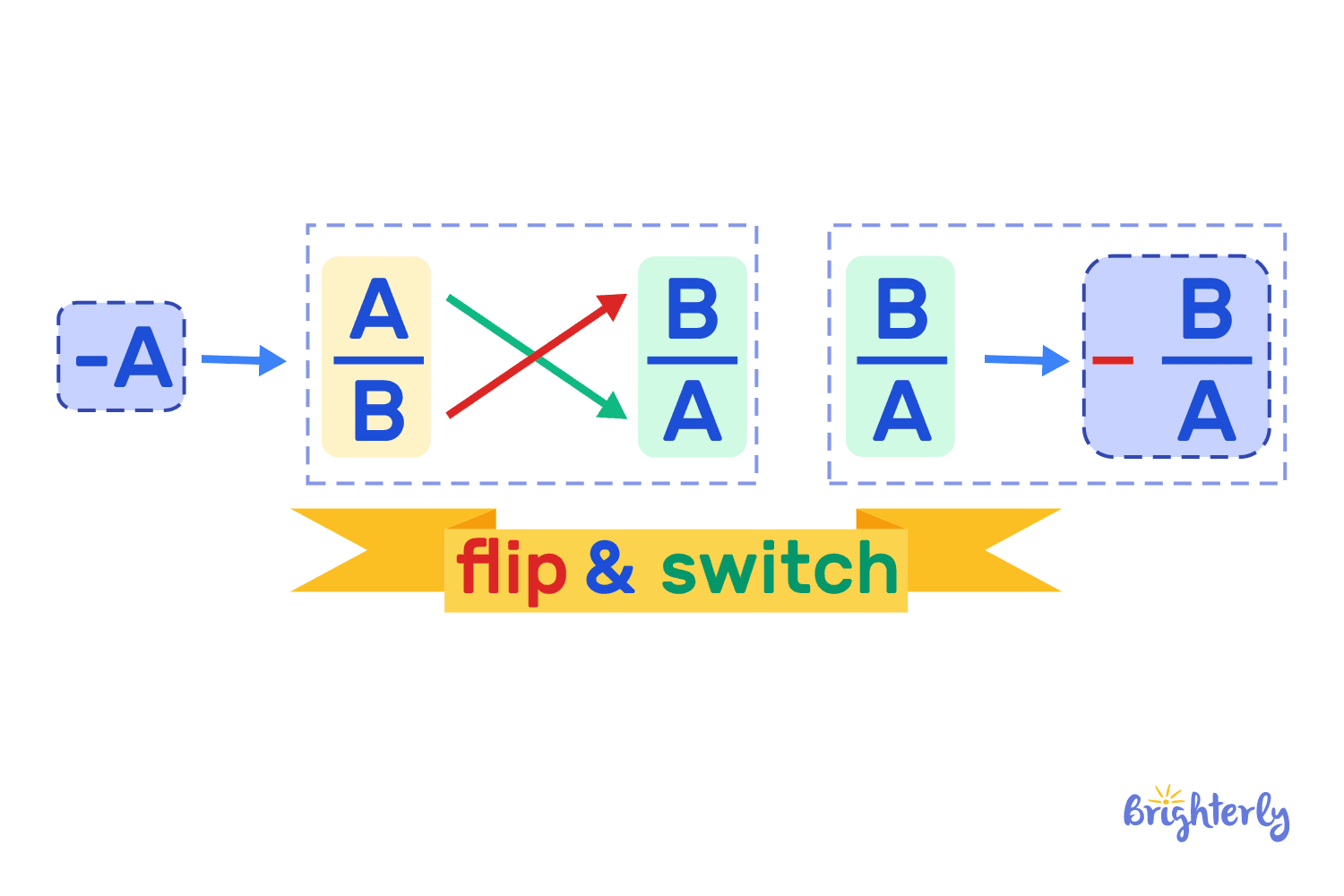
Did you know that negative numbers also have reciprocals? Well, they do, and while finding the reciprocal of a negative number doesn’t differ much from the reciprocal definition of whole numbers. The main difference is, as you may have guessed, the negative sign.
Let’s work through number 4 as an example.
- 4 as a fraction is 4/1
- Reciprocal of 4/1 is 1/4
The process is the same as before. Now, all you have to do is add a negative sign, and you have your negative reciprocal.
An important reminder here: you can flip the numbers and fractions, but the sign cannot be flipped. You cannot turn -4/1 into a 1/4.
What is the reciprocal of 0?
The short answer is, the reciprocal of 0 is undefined. You may remember that one of the key rules of math is that you cannot divide by 0. And finding the reciprocal of a number requires dividing 1 by that number (1/0 in our case), which we cannot do.
Another requirement is that when you multiply the original number by its reciprocal, you get 1. However, there is no number that, when multiplied by 0, yields 1, because anything multiplied by 0 is always 0.
Solved math tasks on reciprocals
1. What is the reciprocal of the number 9?
Solution: Turn to fraction 9/1, then flip to 1/9.
Answer:
| 1/9 |
2. Find the reciprocal of 3/11.
Solution: Flip the fraction to 11/3.
Answer:
| 11/3 |
3. What is the reciprocal of -7?
Solution: Turn to fraction 7/1, flip the fraction to 1/7, and add a negative sign.
Answer:
| – 1/7 |
4. What is the reciprocal of -2/1?
Solution: Flip the fraction -2/1, keep the – sign
Answer:
| -2/1, or simply -2 |
Reciprocal: practice math problems
Frequently asked questions on reciprocals
What is a reciprocal?
Reciprocal meaning in math is the multiplicative inverse of any given number. In simpler terms, the reciprocal of each number is the number you multiply it to get 1. For any number a, its inverse is 1/a. For a negative number -a, the reciprocal is -1/a.
What is an example of a reciprocal in math?
Some examples of a reciprocal of a number are:
- For whole numbers, the reciprocal of 9 is 1/9
- For negative numbers, the reciprocal of -25 is -1/25
- For fractions, the fraction of 11/17 is 17/11
All numbers except for 0 have reciprocals.
How is reciprocal used in math problems?
The most common use of reciprocals in math is in dividing fractions. You can avoid complex divisions by keeping the first fraction, altering the division sign with multiplication, and flipping the second fraction.
How to solve reciprocal?
To find the reciprocal of a number, in the case of whole numbers (and negative whole numbers), you first need to turn the number into a fraction, e.g., 6 becomes 6/1. Then, you flip the fraction, getting 1/6. In case of fractions like 2/3, you simply flip the fraction to 3/2.
How to teach reciprocal in math?
To teach reciprocals, emphasize the importance of getting the answer 1 when multiplying the number and its reciprocal to check their answers. Explain the “turn then flip” method through examples. You can even use visual aids to show that a/b x b/a cancel each other out, and you get 1.
Reciprocal: Worksheets
Reciprocal is not the most straightforward math topic for kids at first, but with a bit of practice, they will both grasp it and see how closely it is connected to other concepts, like fractions. You can help your kid get more relevant practice with their free worksheets:
Winter Math & Reading Camp for Grades 1-9
Join Brighterly's Online Winter Camp to excel in math and reading.
Choose kid's grade
Winter Math & Reading Camp for Grades 1-9
Join our Winter Camp, boost your child's math and reading skills.
