• Math tutors
• /
• Knowledge Base
• /
• Reflexive Property: Definition, Equality, and Practice Math Problems

Reflexive Property: Definition, Equality, and Practice Math Problems

Jessica Kaminski

reviewed by Jo-ann Caballes

Updated on November 13, 2024

Welcome to Brighterly, where we help you understand core math concepts in a way that’s exciting and informative.

Today, we’re going to explore a concept that’s essential to algebra and geometry: reflexive property in math.

Reflexive property helps us understand numbers and shapes and their relationship to themselves.

Here, we’ll cover the reflexive property definition, including the meaning of the reflexive property of congruence and the reflexive property of equality. We also give you the tools and resources to continually improve your learning with free math worksheets and practice test problems.

What is reflexive property?

The reflexive property meaning defines how numbers, shapes, lines and angles are related to themselves. It is made up of three key statements that relate to these areas. At a basic level, reflexive property in math states that any number, shape, line or angle is equal to itself. The three statements of reflexive properties are:

• Reflexive property of congruence
• Reflexive property of equality
• Reflexive property of relations

We define reflexive property and its three specific statements in this article.

Reflexive property example

A straightforward example of reflexive property would be 9 = 9. What we are saying here is that the number 9 is equal to itself, the number 9. We can also use variables – for example, x = x. When it comes to shape, reflexive property states that a shape will be equal to itself – i.e. the same shape and size as itself.

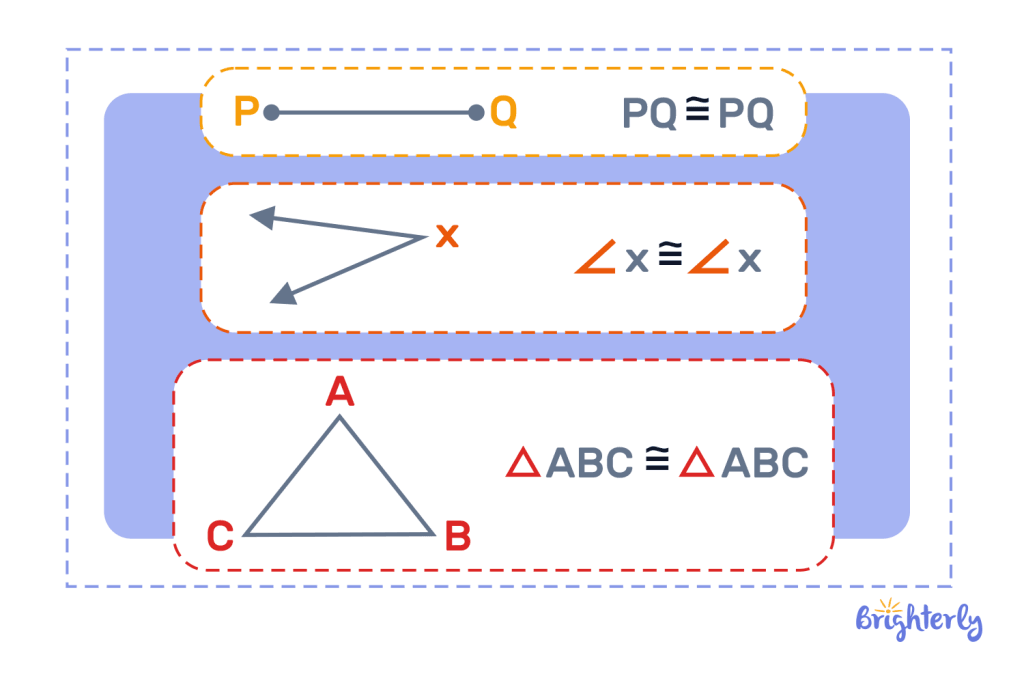
What is the reflexive property of congruence?

The reflexive property of congruence statement defines how geometrical shapes relate to themselves. According to the reflexive property of congruence, any shape, line or angle is identical to itself, meaning it is the same shape and size as itself. We can also say that these shapes are identical to themselves.

The reflexive property of congruence can be used as the basis for a range of mathematical theorems. It’s commonly used to prove that two triangles are congruent. In practice, this means that two triangles that share a common side or angle are congruent to one another, according to the reflexive property of congruence. This is the reflexive property of triangle congruence.

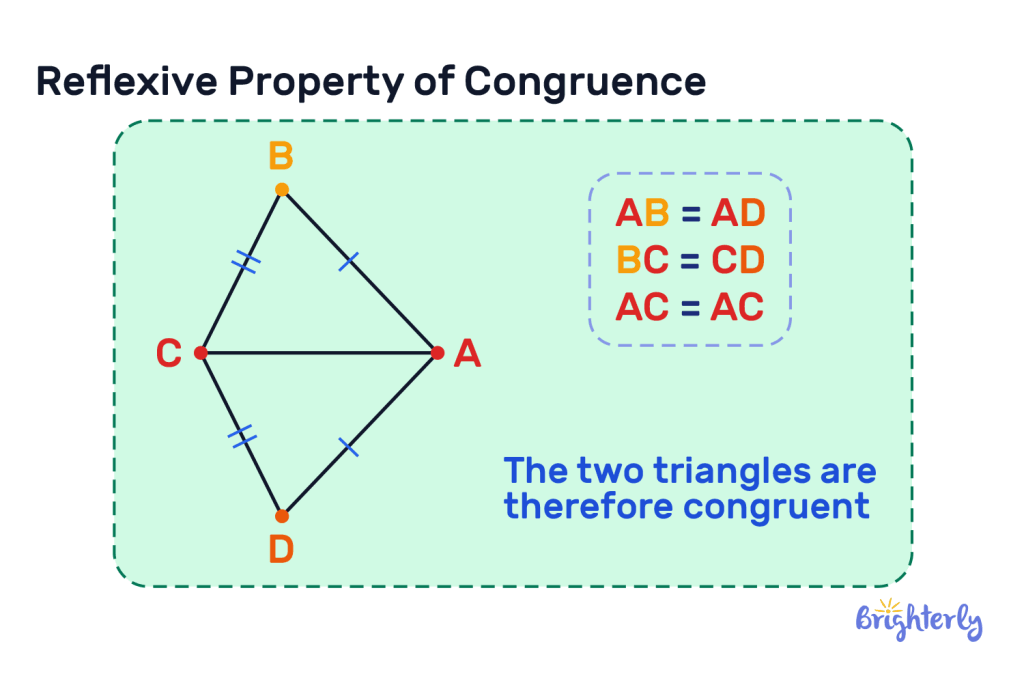
Reflexive property of congruence example

Let’s use the reflexive property of congruence examples to prove two triangles are congruent.

In the figure with triangles ABC and CDA, which share side AC:

• We know that AB = AD and BC = CD.
• Because AC is a side in both triangles, we can say AC = AC by the reflexive property.
• With AB = AD, BC = CD and AC = AC, the two triangles are therefore congruent.

Reflexive property of equality

The reflexive property of equality states that any number or entity is equal to itself. It proves that entities that are the same as one another are of equivalent value and form the basis of many more complex math concepts.

Reflexive property of equality example

An example of the reflexive property of equality would be 4 = 4. We are saying here that 4 is of equal value to itself. We can also use it with algebra and letters, so for example, x = x. We can also use it with multiple and mixed terms – for example, y + 6 = y + 6.

Reflexive property of relations

The reflexive property of relations refers to how elements of an entity relate to the entity as a whole. A relation (which we call R) on a set (which we call A) is called reflexive if every element in AA is related to itself.

In simpler terms, for a relation to be reflexive, each item in the set has to “connect” to itself.

So, if a is an element in the set A, then a should be related to a (written as aRa).

In a set of numbers, the “equal to” relation is reflexive because every number is equal to itself.

Reflexive property of relations example

Let’s use an example with a set of numbers. If we say A = {1,2,3}, a relation (R) is reflexive if each number is related to itself.

Let’s define R as “is equal to”:

• 1 is equal to 1 (so (1,1) is in R)
• 2 is equal to 2 (so (2,2) is in R)
• 3 is equal to 3 (so (3,3) is in R)

Since every element in A is related to itself, R is a reflexive relation on the set A.

Solved math tasks: examples

Ready to put your knowledge of reflexive property in math to the test? We’ve included a range of solved math problems below – simply work out each problem, then check them against our answers. How many did you get right?

Solved math task 1

We have a line that measures 8 cm. If we have another line that is congruent to this line, how long does this line measure?

Answer: 

Using the reflexive property of segment congruence, we know that congruent lines are the same length as one another. Therefore, our line’s congruent line is also 8 cm long.

Solved math task 2:

Tim has 3 pieces of candy in his left hand. How many pieces of candy does he need to have in his right hand for the two to be equal?

Answer:

Because every number is equal to itself and we need an equal number of candies in his other hand, we also need him to have 3 candies in his right hand.

Reflexive property: worksheets

To become a true master of reflexive property, you need to hone your understanding of it through continued practice. Check out our cool math worksheets below – not only are they educational, but they are fun to work with!

• Triangle congruence worksheets
• Similar triangles worksheets
• Linear equation in one variable worksheets
• Geometry worksheets

Jessica Kaminski

70 articles

Jessica is a a seasoned math tutor with over a decade of experience in the field. With a BSc and Master’s degree in Mathematics, she enjoys nurturing math geniuses, regardless of their age, grade, and skills. Apart from tutoring, Jessica blogs at Brighterly. She also has experience in child psychology, homeschooling and curriculum consultation for schools and EdTech websites.