• Math tutors
• /
• Knowledge Base
• /
• Side Angle Side: Definition, Congruence, Examples

Side Angle Side: Definition, Congruence, Examples

Jessica Kaminski

reviewed by Jo-ann Caballes

Updated on October 8, 2024

At Brighterly, it’s our mission to make math engaging, fun and easy to learn for kids of all ages.

Today we will be covering the side angle side theorem, a fascinating theory related to the sides and angles of triangles.

We’ll cover the definition of the side angle side theorem and triangle congruence theorems, and provide examples and practice test questions so you can put your new-found knowledge to the test.

What Is the SAS theorem in geometry?

The SAS theorem in geometry is a theory that explains the relationships between two triangles with corresponding lengths and angles of the same length and angle. Below, we cover the SAS definition.

Math tutors

Improve your child’s math skill today with Brighterly

Let them be at the top of their class.

Book free lesson

Side angle side definition in geometry

The side-angle-side definition in geometry is as follows: if two triangles have two corresponding sides that are the same length, plus the angles between these sides (also known as included angles) are equal, the two triangles are congruent. In other words, they have the same shape and size.

A similar theorem is the angle side angle theorem, which states that if two triangles have two of the same corresponding angles, and the connecting sides are the same length, they are also congruent. So if you’re wondering, “Is SAS congruent?”, the answer is yes.

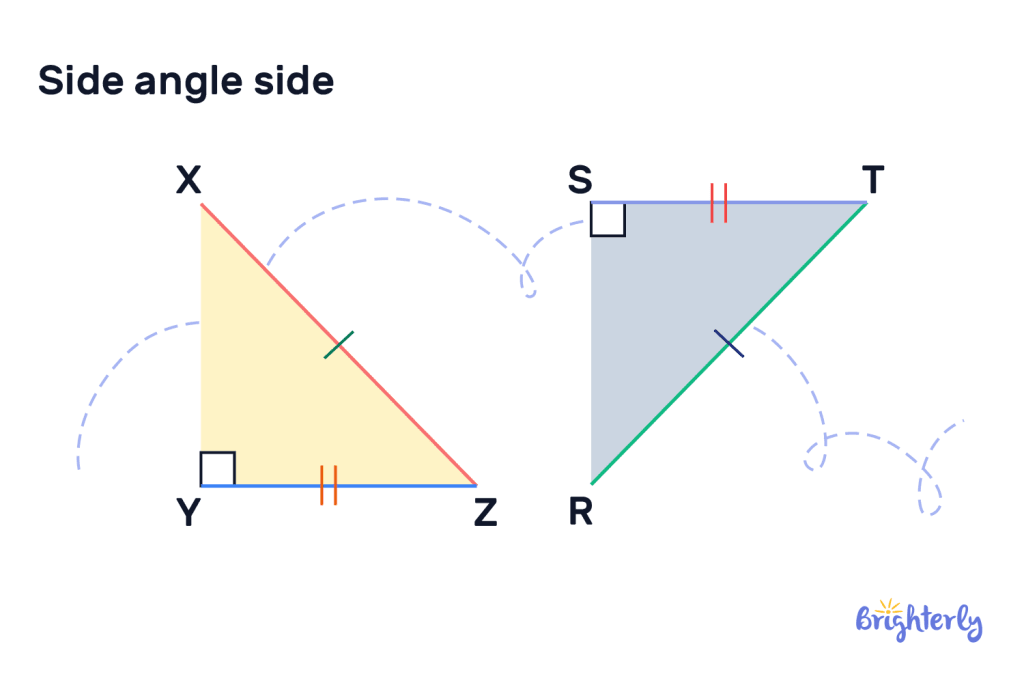
What is SAS similarity?

SAS similarity is a theorem or test that highlights triangles that are similar but not congruent. If two triangles have corresponding side lengths of the same ratio, and the angles on those sides of both triangles are the same, the triangles are the same shape but are different sizes.

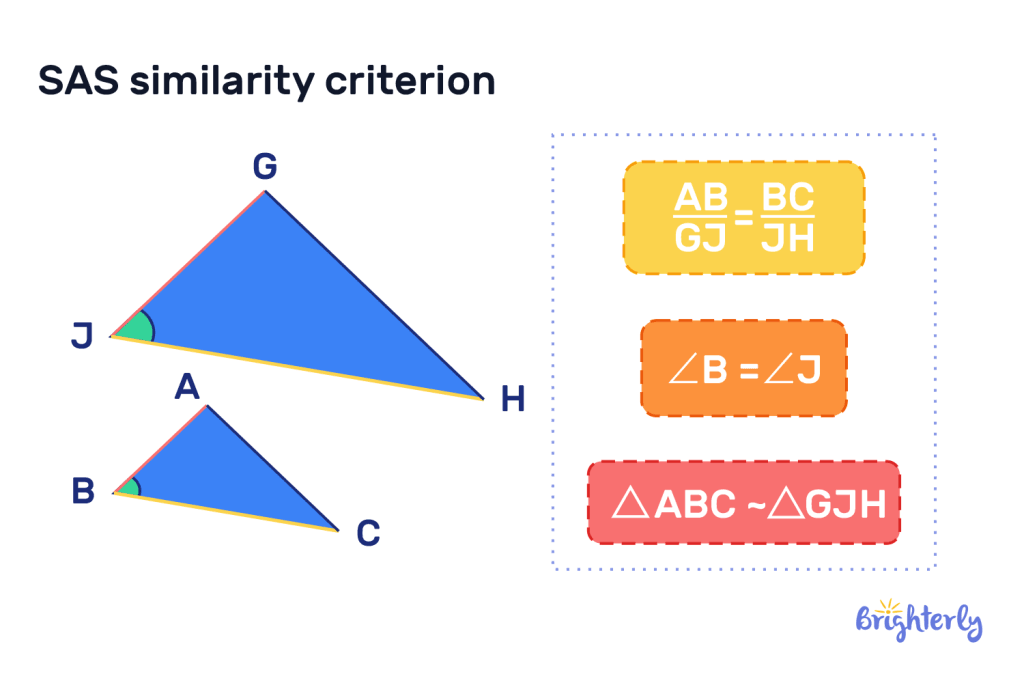
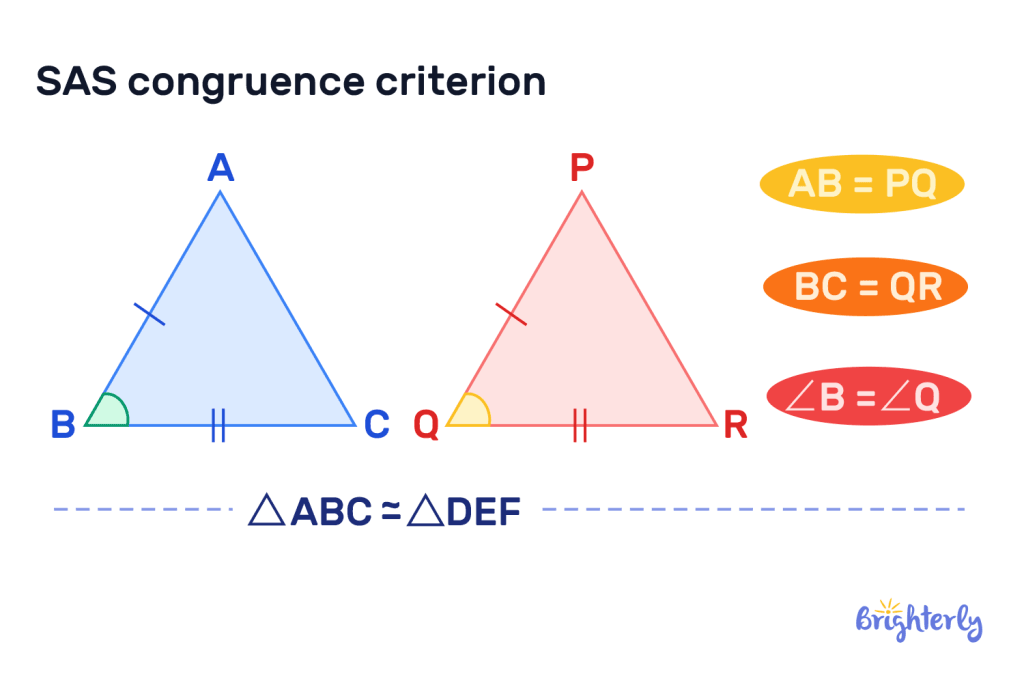
Side-angle-side congruence theorem

The side-angle-side congruence theorem is another name for SAS in geometry, which states that two triangles are congruent if:

• They have two sets of corresponding sides of the same length
• The angles between those corresponding sides are the same across both triangles

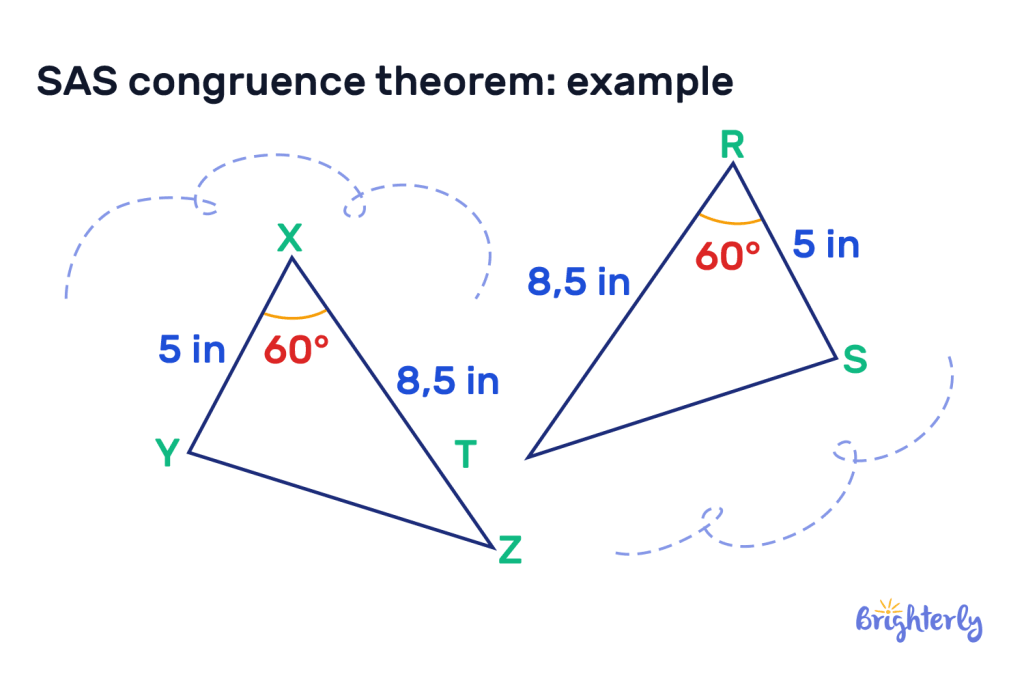
SAS congruence theorem: example

Let’s take the example of two triangles that both have corresponding lengths of 5 inches and 8.5 inches, and the internal angle of those two sides is 60°. In this example, the triangles are congruent – i.e. they are the same shape and size.

SAS similarity rule

The SAS similarity rule states that if two triangles have two corresponding sides that are proportionate, with an internal angle that is the same across both sides, they are the same shape but in different sizes.

SAS similarity theorem: example

Here’s a SAS similarity theorem example. You have one triangle with two sides of 3cm and 6cm, with an angle of 45° between them. The second triangle has two sides of 6cm and 12cm, with an angle of 45° between them. Both of these triangles would have SAS similarity because they’re of the same ratio.

Solved math tasks: examples

Here, we’ve included some solved math SAS triangle examples so you can practice your new-found knowledge of the SAS meaning.

Solved math task 1

If you have one triangle with two corresponding sides of 5cm and 8cm, with an internal angle of 90°, and a second triangle with corresponding sides of 10cm and 16cm and an angle of 90°, are they SAS triangles?

Answer:

This is because 5cm and 8cm are proportionate to 10cm and 16cm.

Solved math task 2

Measure the lengths of the sides of these triangles and measure the marked-up internal angles with a protractor. Are they SAS triangles?

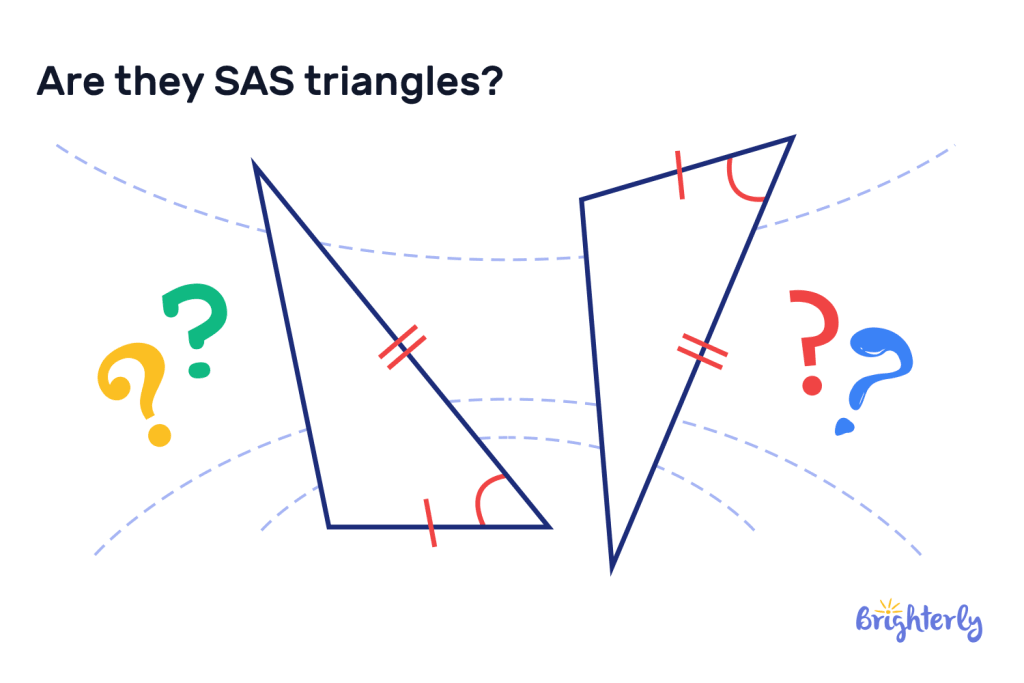
Answer:

Side angle side: practice math problems

Side angle side: worksheets

Now that you’ve learned about side-angle-side theorems, put your knowledge to the test with our engaging math worksheets:

• Triangle congruence worksheets
• 45-45-90 and 30-60-90 triangle worksheets
• Similar triangles worksheets
• Types of triangles worksheets

Jessica Kaminski

67 articles

Jessica is a a seasoned math tutor with over a decade of experience in the field. With a BSc and Master’s degree in Mathematics, she enjoys nurturing math geniuses, regardless of their age, grade, and skills. Apart from tutoring, Jessica blogs at Brighterly. She also has experience in child psychology, homeschooling and curriculum consultation for schools and EdTech websites.