• Math tutors
• /
• Knowledge Base
• /
• Supplementary Angles – Definition With Examples

Supplementary Angles – Definition With Examples

Jessica Kaminski

reviewed by Jo-ann Caballes

Updated on October 21, 2024

Welcome to another fascinating exploration of the universe of mathematics with Brighterly, your reliable partner in making learning not just easy, but also fun and engaging! 

Today, we’re going to cover a key concept in geometry and shapes: supplementary angles. Understanding, identifying and measuring supplementary angles is not only fundamental to math but also has benefits to our everyday life – whether we’re looking at a half-eaten pizza or the hands on a clock, we see them everywhere!

Here, we’ll cover the supplementary angles meaning, how many degrees they add up to and how to find a supplementary angle. To help you practice your learning, we’ll also give you cool free math worksheets and practice questions!

What are supplementary angles?

The supplementary def math is two angles – i.e. a pair of angles – whose combined total equals 180°. If any angles in a shape combine to make 180°, they are classed as supplementary angles. Even a simple straight line divided into two parts by another line forms two angles that are supplementary.

For example, the two angles below both total 180° (130° + 50° = 180°), therefore they are supplementary angles.

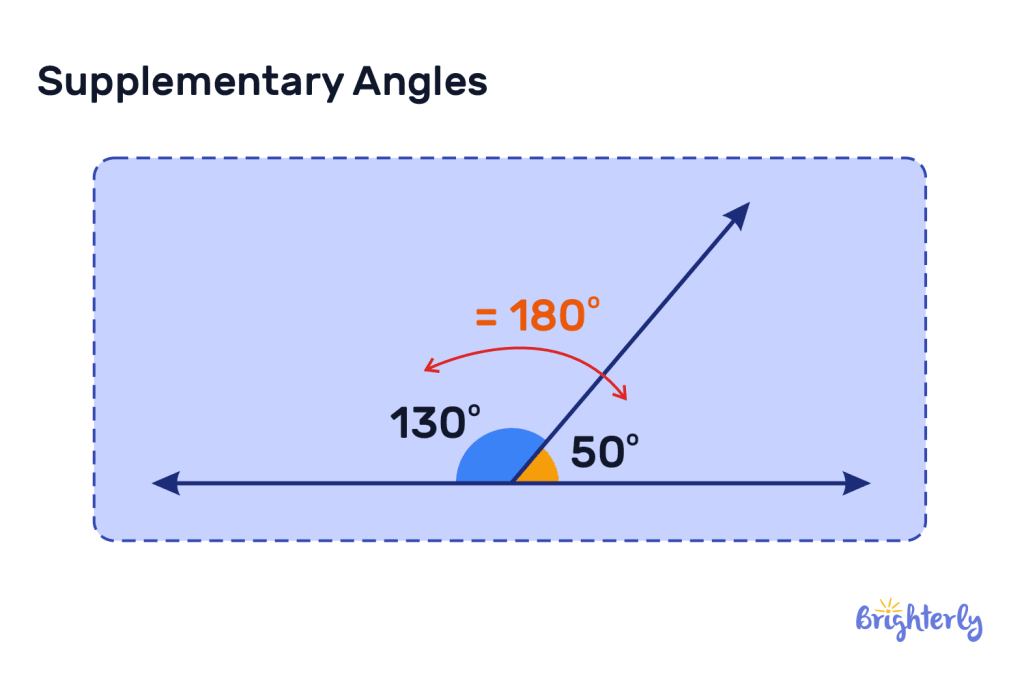
What does a supplementary angle look like?

Supplementary angles come in many forms, but generally speaking they will be formed by a straight line and an intersecting line at the minimum. They can be found in both shapes and in line segments. These angles complete one another, forming a perfect half circle or a straight angle. 

Here’s an example of supplementary angles.

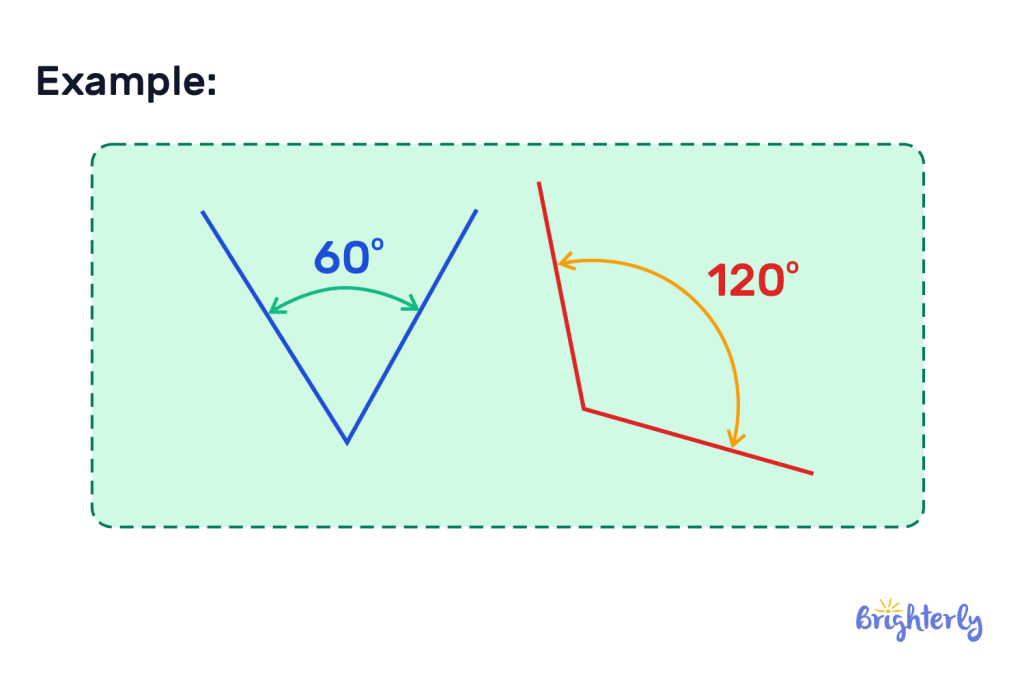
How many degrees do supplementary angles add up to?

Supplementary angles will always add up to 180°. This is the main defining property of supplementary angles, so if you have two angles whose sum doesn’t add up to 180°, they are not supplementary angles. 

Math tutors

Improve your child’s math skill today with Brighterly

Let them be at the top of their class.

Book free lesson

What are adjacent and non-adjacent supplementary angles?

Did you know there are different types of supplementary angles?

We have both adjacent and non-adjacent supplementary angles. We’ll explain both of these types of angles and share images of supplementary angles below.

Adjacent supplementary angles

Adjacent supplementary angles share a vertex, and they also have a common arm.

In the supplementary angles example below, we can see the shared vertex (O) and the shared arm (OB) of these two supplementary angles.

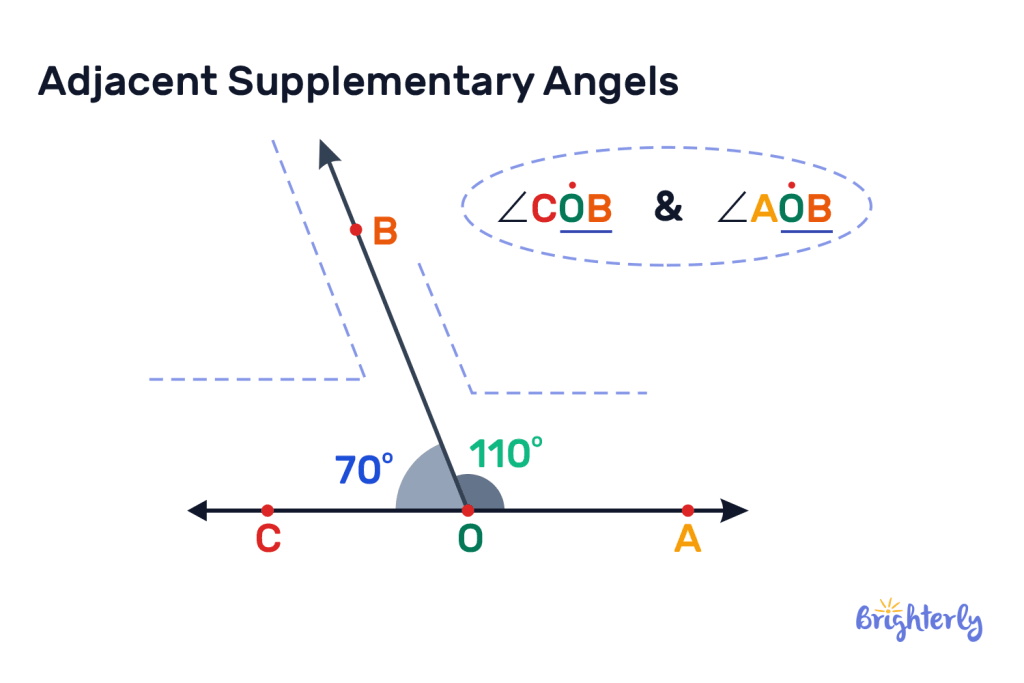
Non-adjacent supplementary angles

Non-adjacent supplementary angles, meanwhile, do not share a vertex or an arm. They still add up to 180°, but they are two separate angles. You’ll most likely find non-adjacent supplementary angles inside closed shapes such as squares, rectangles, trapezoids and some triangles. Here are some supplementary angles that are not adjacent.

How do you find a supplementary angle?

In order to find your supplementary angles, you can either use a protractor or you can find a missing angle if you know the measure of your other angle. In that case, all you need to do is subtract your known angle from 180° to find your missing supplementary angle.

This can be represented by a very straightforward formula: y = 180° – x.

If we take the below supplementary angles example, we can find x by taking 118° away from 180°.

180° – 118° = 62°.

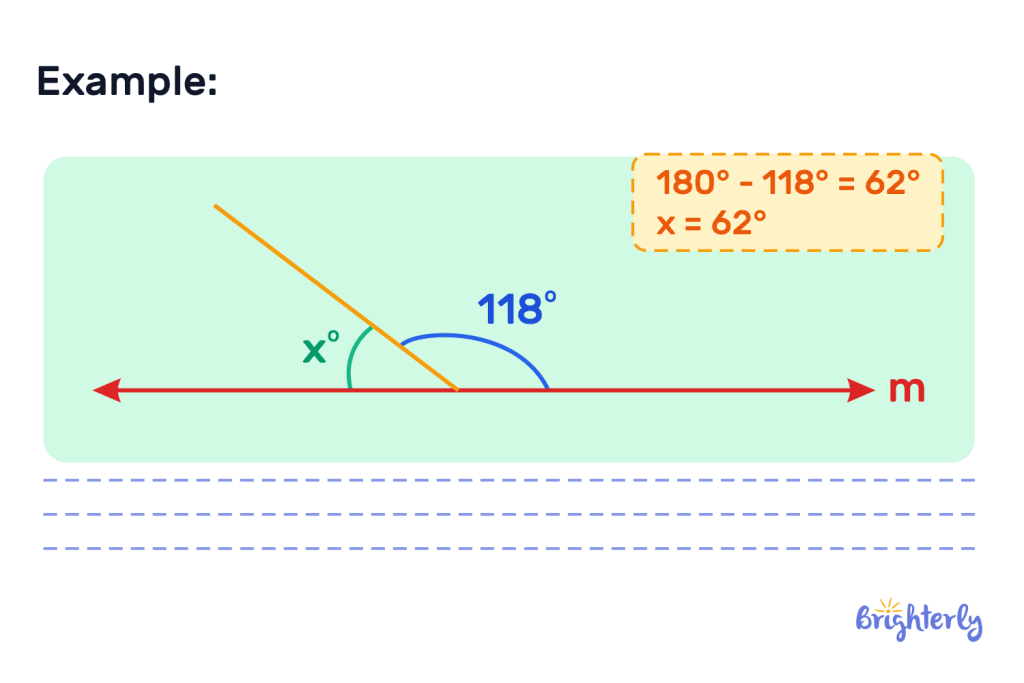
Facts about supplementary angles

There are some interesting facts about supplementary angles that are important to know. These are also referred to as properties – attributes that make supplementary angles distinct from other types of angles.

• The sum of 2 supplementary angles will always be 180°
• When put together, supplementary angles make a straight line, but they do not need to be together to be supplementary
• If two angles are supplementary to the same angle, those two angles are congruent (i.e. they have the same measure)
• If a line is perpendicular to 1 of 2 supplementary angles, it is also perpendicular to the other

Solved math tasks: examples

Are you ready to test yourself on your ability to understand and work out supplementary angles? Try out our math tasks below – we’ve already solved them, so work out your answers then check them against the real answers to see how you’ve done!

Solved math task 1

You have two supplementary angles, and one measures 121°. How much does your missing supplementary angle measure?

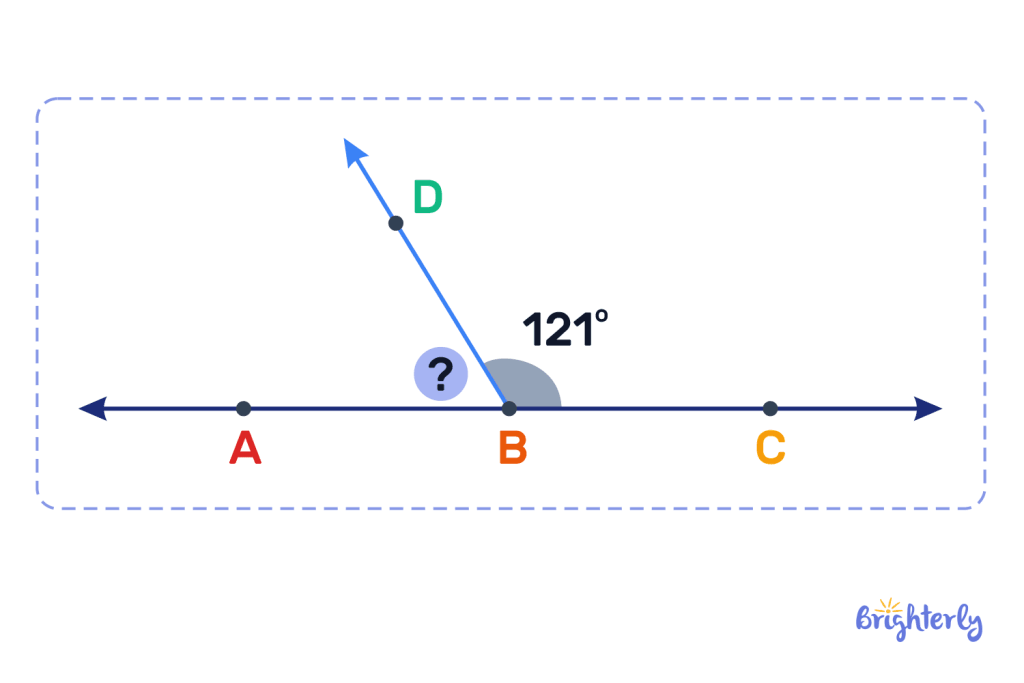
Answer:

To find this missing angle, you need to take your known supplementary angle away from 180°.

180° – 121° = 59°

Solved math task 2

You have two supplementary angles below. Are they adjacent or non-adjacent? Tell us how you know.

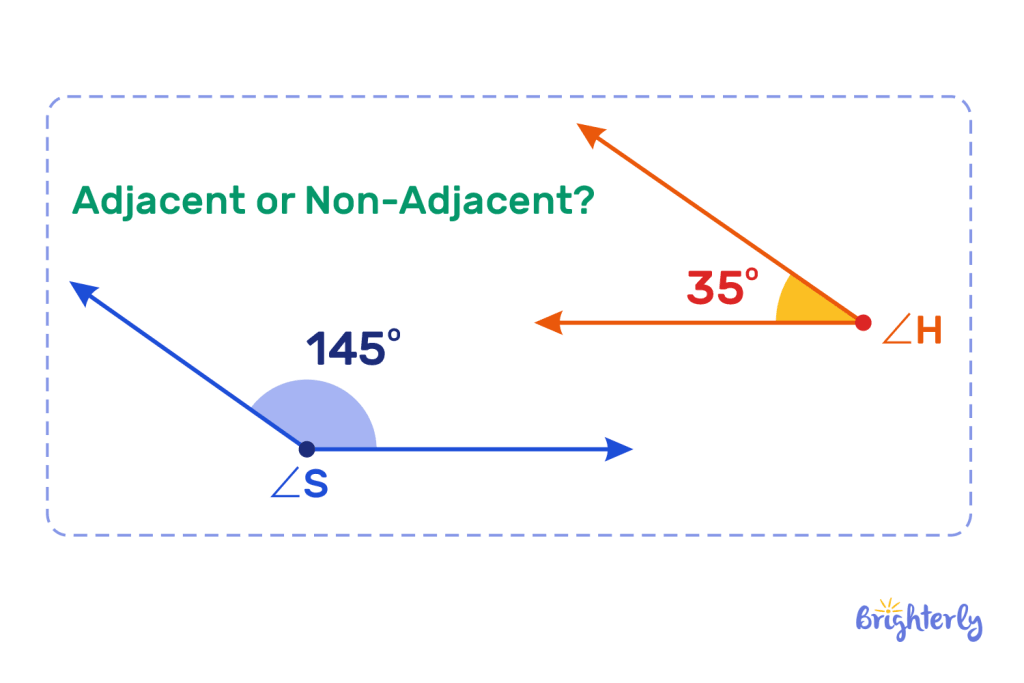
Answer:

That’s because they don’t share a vertex or an arm.

Solved math task 3

Which of the following pairs of angles could be classed as supplementary?

• 30°, 75°
• 45°, 83°
• 60°, 120°
• 72°, 91°

Answer: 

That’s because their sum equals 180°.

Supplementary angles: practice math problems

Supplementary angles: worksheets

Are you ready to put your knowledge on supplementary angles to the test? Try out our fun and challenging worksheets on supplementary angles and more!

• Angles worksheets
• Measuring angles worksheets
• Pairs of angles worksheets
• Measuring angles with a protractor worksheets

Jessica Kaminski

70 articles

Jessica is a a seasoned math tutor with over a decade of experience in the field. With a BSc and Master’s degree in Mathematics, she enjoys nurturing math geniuses, regardless of their age, grade, and skills. Apart from tutoring, Jessica blogs at Brighterly. She also has experience in child psychology, homeschooling and curriculum consultation for schools and EdTech websites.