Vertical Angles – Theorem, Definition With Examples
Updated on November 3, 2025
Geometry is a fascinating branch of math, and we’re here to help you understand it.
Today, we’re exploring vertical angles. These congruent angles lie opposite one another.
Here, we’ll define vertical angles, their theorem and the properties of these angles. We’ll also give you examples of vertical angles and share some practice problems so you can put your newfound knowledge on vertical angles to the test!
What are vertical angles?
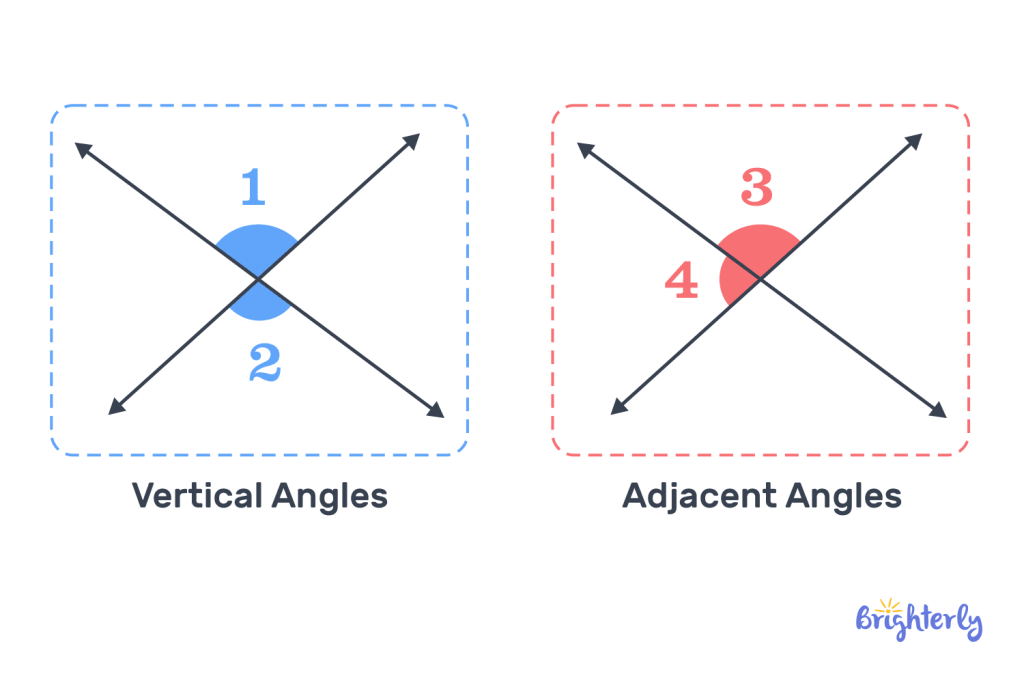
Vertical angles are angles opposite one another on two intersecting lines. If you draw an X shape with two intersecting lines, the pairs of angles opposite one another that don’t share a vertex are vertical angles. If you’re asking, “Are vertical angles congruent?”, the answer is yes.
Definition of vertical angles
The definition of vertical angles is pairs of angles that are opposite one another at the point of two lines intersecting. When two lines intersect, they create 4 angles, meaning there are 2 pairs of vertical angles. In the X shape, they are the two angles on the side of the intersect, and the angles above and below.
Vertical angles theorem
The vertical angles theorem states that all vertical angles created by 2 intersecting lines are vertical angles congruent — i.e. equal to one another. You will never find a pair of vertical angles created by two lines intersecting that are not congruent.
Properties of vertical angles
Vertical angles have some properties that help define them and separate them from other angles:
- They are always equal to one another: All vertical angles are congruent, meaning they have the same measurement
- They are always next to supplementary angles: All vertical angles share a vertex with a supplementary angle, which, when added to your vertical angle, will always make 180°
Vertical angles examples
We’ve already looked at the example of vertical angles in an X shape, so let’s explore some more. A line that intersects in a + shape will also create vertical angles, but what’s interesting about this is that they will all be the same measurement — 90° right angles. But even though all angles are congruent, the vertical angle theorem and properties still apply.
Proving the vertical angles theorem
We can prove the vertical angles congruence theorem by drawing different intersecting lines and measuring their angles. Every time you do this, you’ll find that vertical angles are always congruent, and always share a vertex with a supplementary angle.
Comparison between vertical angles and other types of angles
Supplementary angles |
Adjacent angles |
Complementary angles |
| These angles differ to vertical angles because they share a vertex with vertical angles and they will always add up to 180° | These angles differ to vertical angles because they too share a vertex, but they do not need to add up to 180° | These angles differ to vertical angles because they always add up to 90°, share a vertex and are created by splitting a right angle |
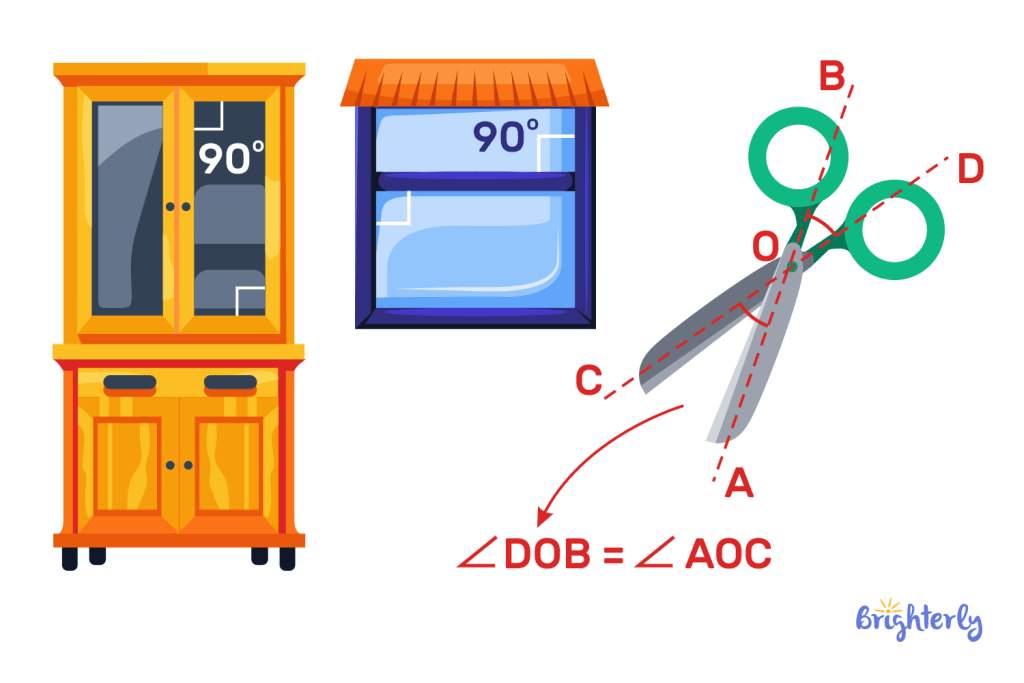
Vertical angles in real life
There are lots of vertical angles real life examples, including:
- A pair of scissors
- Intersecting roads or streets
- A railroad crossing sign
Equations involving vertical angle theorem
Equations involving the vertical angle theorem will always be balanced, even if each side of the equation is not the same.
For example, if you know one of your vertical angles is equal to 3x x 5 and your opposite vertical angle is equal to x + 10, your equation becomes 3x x 5 = x + 10.
Writing equations based on vertical angles
To write equations based on the known values of vertical angles, you simply show that your vertical angles are equal to one another.
Let’s use another example. One vertical angle is equal to 2y x 3 and its pair is equal to y + 6. Therefore, our equation is 2y x 3 = y + 6.
Vertical angles: Practice problems
Now it’s your turn to give vertical angle puzzles a go. Simply write down your answers to the following practice problems down, using all the knowledge you’ve learnt in this article.
- One angle in two intersecting lines is given as (3x – 10) degrees, and its vertical angle is (2x + 20) degrees. Work out the value of x and the measure of the angles.
- You have two vertical angles that both measure 65°. What is the measure of their supplementary angles?
Conclusion
Now you know all about the vertical angles meaning, you can apply this knowledge to your geometry classes and also try to spot vertical angles in your everyday life!
Learning about vertical angles sets you up for a successful journey in geometry and math.
Vertical angles: Frequently asked questions
What is a vertical angle?
A vertical angle is an angle created by 2 intersecting lines. It will have another vertical angle opposite that it doesn’t share a vertex with, and both angles will be equal in measure.
What do vertical angles add up to?
There is no set value that pairs of vertical angles add up to. However, vertical angles are always equal to one another, and when combined with the second pair of vertical angles, will always add up to 360°.
Are vertical angles always equal?
Yes, vertical angles are always equal. This is dictated by the vertical angles theorem, which states that all pairs of vertical angles are congruent (equal).
How are vertical angles used in real life?
Vertical angles can be used in real life in a number of ways. Astronomers make use of vertical angles when calculating the positioning of celestial bodies like stars, while pool players can use them to calculate the angles of their shot.
Can vertical angles be supplementary?
No, vertical angles cannot be supplementary. This is because they are always opposite one another, while they share a vertex with supplementary angles.






