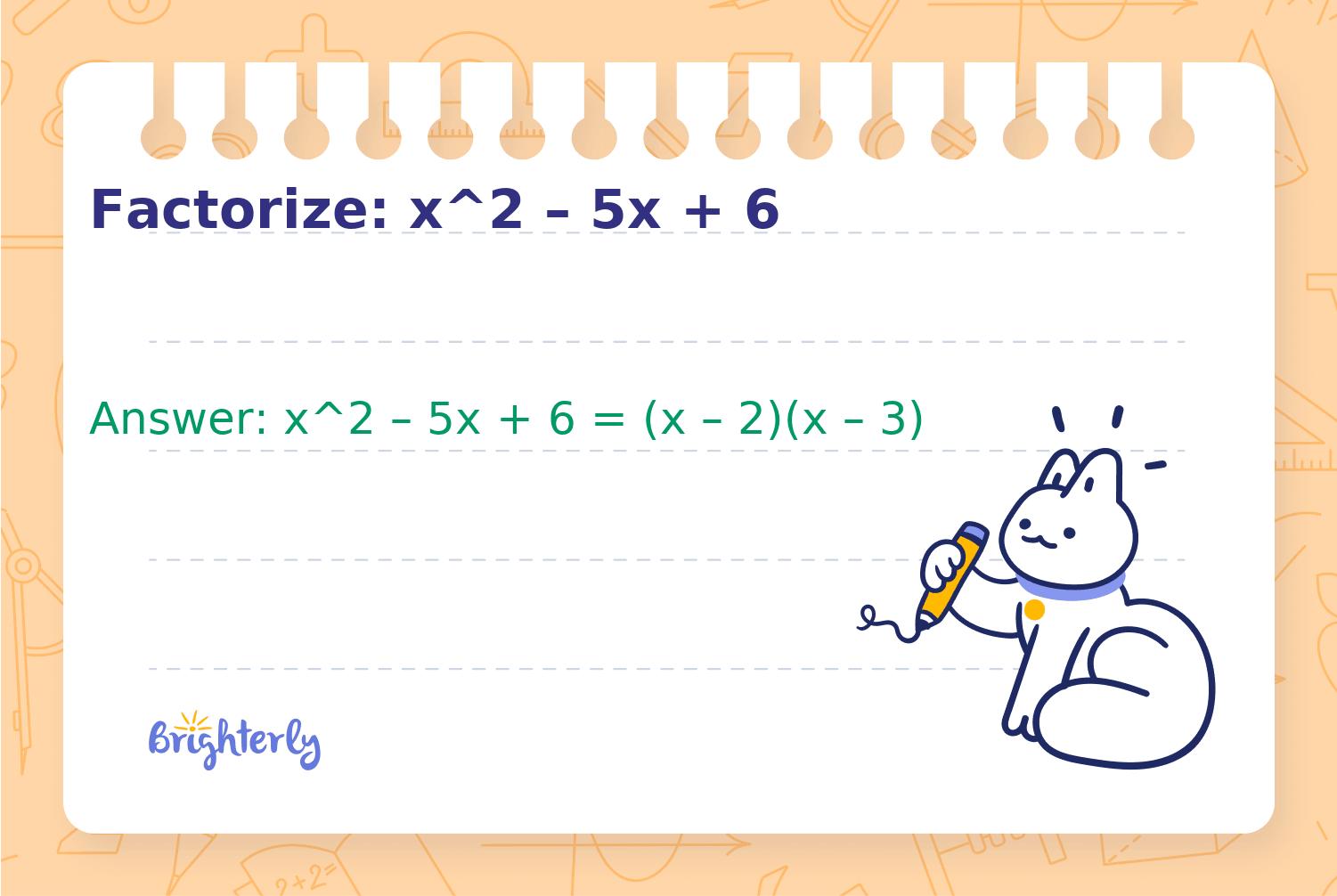Reviewed by Phoebe Belza-Barrientos
Factorize: x^2 – 5x + 6
Answer: x^2 – 5x + 6 = (x – 2)(x – 3)
Quadratic expressions like x^2 – 5x + 6 can often be rewritten as a product of two binomials through a process called factorization. This is an important algebraic technique used to simplify expressions and solve equations.
Methods
Math Tutor Explanation Using the Middle Term Splitting Method
This method involves finding two numbers that multiply to the constant term and add up to the coefficient of the middle term.
Step 1: Step 1: Identify two numbers that multiply to 6 (the constant term) and add up to -5 (the coefficient of x)
Step 2: Step 2: The numbers -2 and -3 fit because (-2) × (-3) = 6 and (-2) + (-3) = -5
Math Tutor Explanation Using the Quadratic Formula Method
This method involves finding the roots of the quadratic and expressing the equation in factored form.
Step 1: Step 1: Use the quadratic formula: x = [-b ± √(b^2 – 4ac)] / 2a, where a = 1, b = -5, c = 6
Step 2: Step 2: Find the roots: x = [5 ± √(25 – 24)] / 2 = [5 ± 1] / 2, giving x = 3 and x = 2
Step 1:
Step 2:
Math Tutor suggests: Practice Factoring Quadratic Equations
If you want to strengthen your factoring skills, try these related exercises involving factoring quadratics and working with similar algebraic concepts.
FAQ on Factoring Quadratics
How can you check your factorization?
Expand the factors; if they multiply back to the original quadratic, your factorization is correct.
What do you do if the quadratic cannot be factored with integers?
Use the quadratic formula or complete the square to find the roots.
Why is factoring quadratics useful?
It simplifies solving equations and reveals the roots directly.
Can every quadratic be factored?
Every quadratic can be factored over the complex numbers, but not every one factors nicely with real or integer coefficients.
Math & reading from 1st to 9th grade
Looking for homework support for your child?
Choose kid's grade
