Reviewed by Mary Grace Carlos
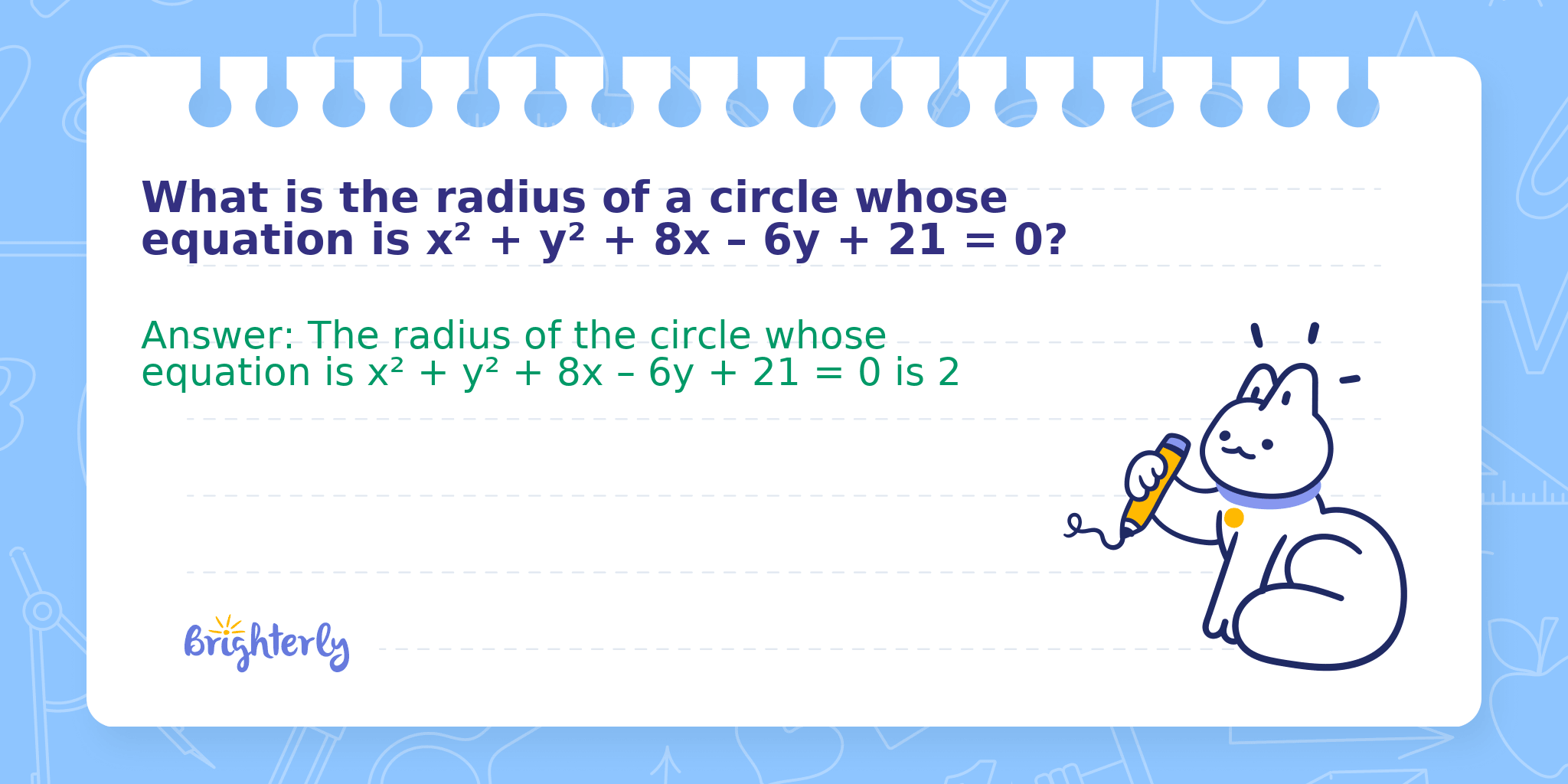
What is the radius of a circle whose equation is x² + y² + 8x – 6y + 21 = 0?
Answer: The radius of the circle whose equation is x² + y² + 8x – 6y + 21 = 0 is 2
The equation x² + y² + 8x – 6y + 21 = 0 represents a circle in standard form. To determine the circle's radius, we need to rewrite the equation in the standard form of a circle: (x – h)² + (y – k)² = r², where (h, k) is the center and r is the radius. This process involves completing the square for both x and y terms.
Methods
Math Tutor Explanation Using Completing the Square Method
We convert the given equation into the standard circle equation by completing the square for x and y, allowing us to identify the radius.
Step 1: Group x and y terms: (x² + 8x) + (y² – 6y) = –21
Step 2: Complete the square for x and y: (x² + 8x + 16) + (y² – 6y + 9) = –21 + 16 + 9
Math Tutor Explanation Using Comparison to Standard Circle Equation
Compare the rearranged equation to the standard form to directly find the radius.
Step 1: Bring the equation to the form (x + 4)² + (y – 3)² = r²
Step 2: Recognize that (x + 4)² + (y – 3)² = 2², so the radius is 2
Step 1:
Step 2:
Math Tutor suggests: Explore More Circle Equations and Properties
Deepen your understanding of circles in algebra by checking out these related questions about circle equations, radii, and special parts of a circle.
FAQ on Finding the Radius and Center of a Circle from Its Equation
How do you convert a general circle equation to standard form?
Complete the square for both x and y terms and rearrange to match (x – h)² + (y – k)² = r².
What is the formula for the radius once the standard form is obtained?
The radius is the square root of the constant on the right side of the standard form equation.
Can the radius be negative?
No, the radius of a circle is always a positive real number.
How do you find the center of the circle from the equation?
The center is given by (h, k) from the standard form (x – h)² + (y – k)² = r².
Math & reading from 1st to 9th grade
Looking for homework support for your child?
Choose kid's grade
