• Math tutors
• /
• Knowledge Base
• /
• Cross Multiplication: Definition and Practice Problems

Cross Multiplication: Definition and Practice Problems

Camille Ira B. Mendoza

reviewed by Jo-ann Caballes

Updated on October 28, 2024

Welcome to the world of Brighterly, where we simplify math concepts to turn you into a mathematics expert!

Today, we’re going to delve into the world of fractions and discuss cross multiplication.

Cross multiplication is a key method of simplifying fractions and making them easier to work with – by mastering this method, you can also master working with fractions!

Here, we’ll cover the cross multiplication definition, show you how to cross multiply, and provide cross multiplication examples. We’ll also finish with some practice math problems and downloadable worksheets so you can test yourself!

What is cross multiplication?

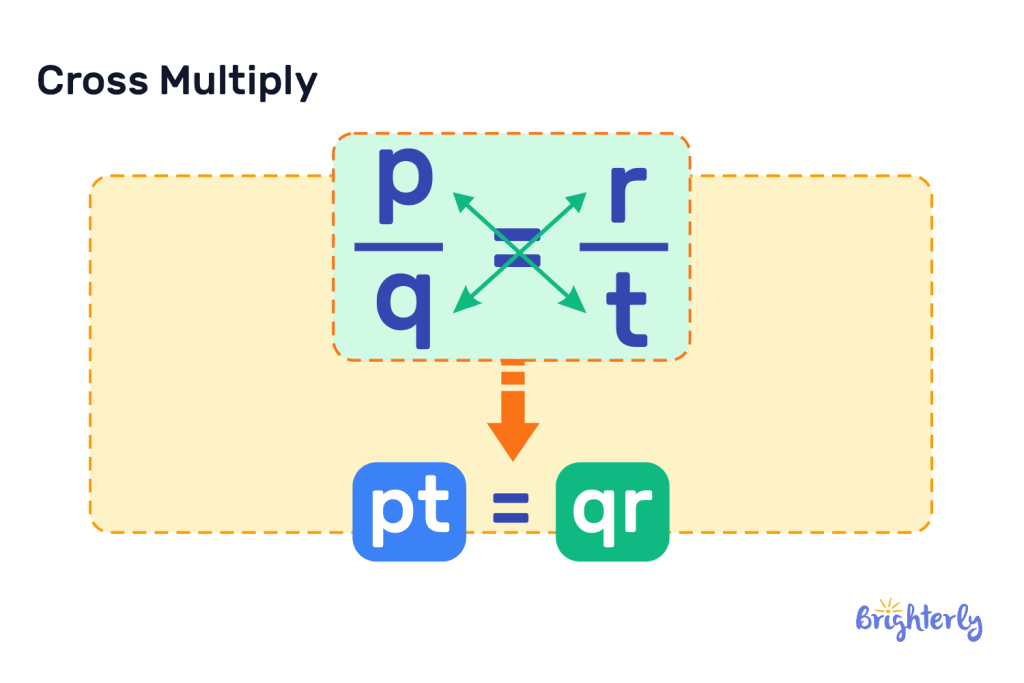
Cross multiplication involves multiplying numerators and denominators in two different fractions. It’s a method that helps us to compare and work with fractions, and we can even turn unlike fractions into like fractions.  You can cross multiply and divide fractions. Find the full definition of cross multiplication below.

Multiplying fractions definition

Cross multiplication, also known as multiplying fractions, is the act of multiplying the numerator in one fraction by the denominator of the other fraction. By cross multiplying fractions, we can more easily compare them and determine variables within fractions.

Cross multiplication example

Let’s take the example of ⅔ and 4/6. First, we cross multiply the first fraction numerator with the second fraction denominator, then multiply the first fraction denominator by the second fraction numerator. 

• 2 x 6 = 12
• 3 x 4 = 12

12 = 12.

This means both fractions are equal in value!

How to cross multiply fractions?

To cross multiply fractions, you would first multiply the numerator in your first fraction by the denominator in your second fraction. Then, multiply the denominator in your first number by the numerator in your second fraction. This is the cross multiplication method.

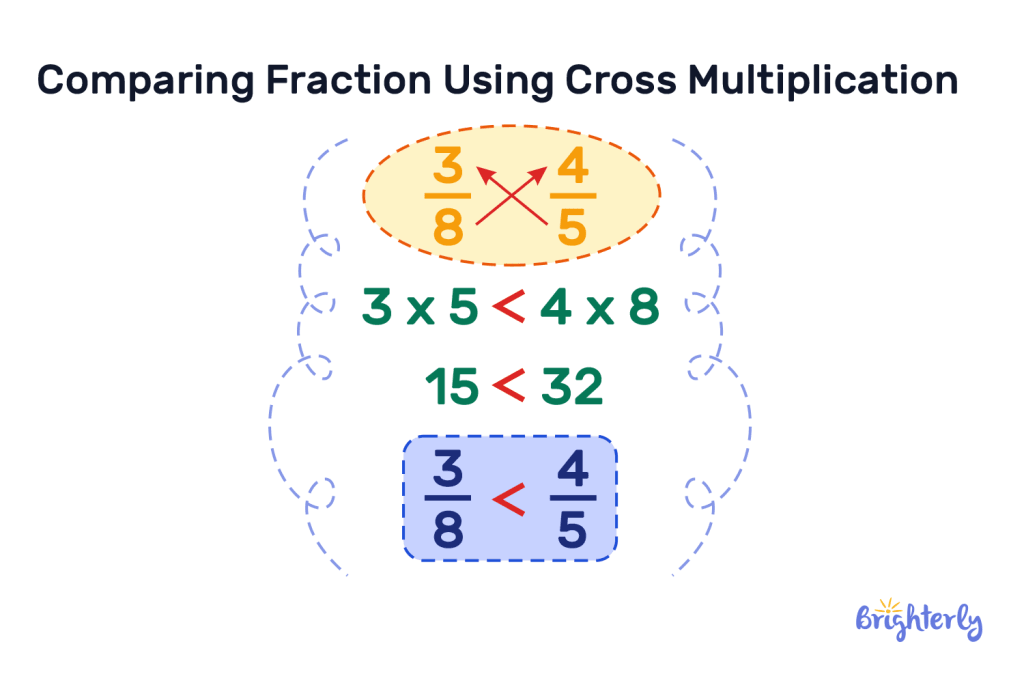
Cross multiply fractions to compare unlike fractions

If you have two unlike fractions that you need to compare, you can do this via cross multiplication.

Let’s use the example of ⅔ and ⅗. First, multiply your first numerator by your second denominator.

2 x 5 = 10.

Then, multiply your first denominator by your second numerator.

3 x 3 = 9.

Next, compare your two results. 10 is larger than 9, so we can confidently say that the fraction ⅔ is larger than the fraction of ⅗.

This can be a faster method of comparing fractions than finding common denominators.

Why does cross multiplication work?

Cross multiplication works by canceling out denominators, leaving only numerators. By multiplying opposite numerators with denominators, you are effectively comparing the numerators only by creating common denominators, without the additional step of finding the common denominators.

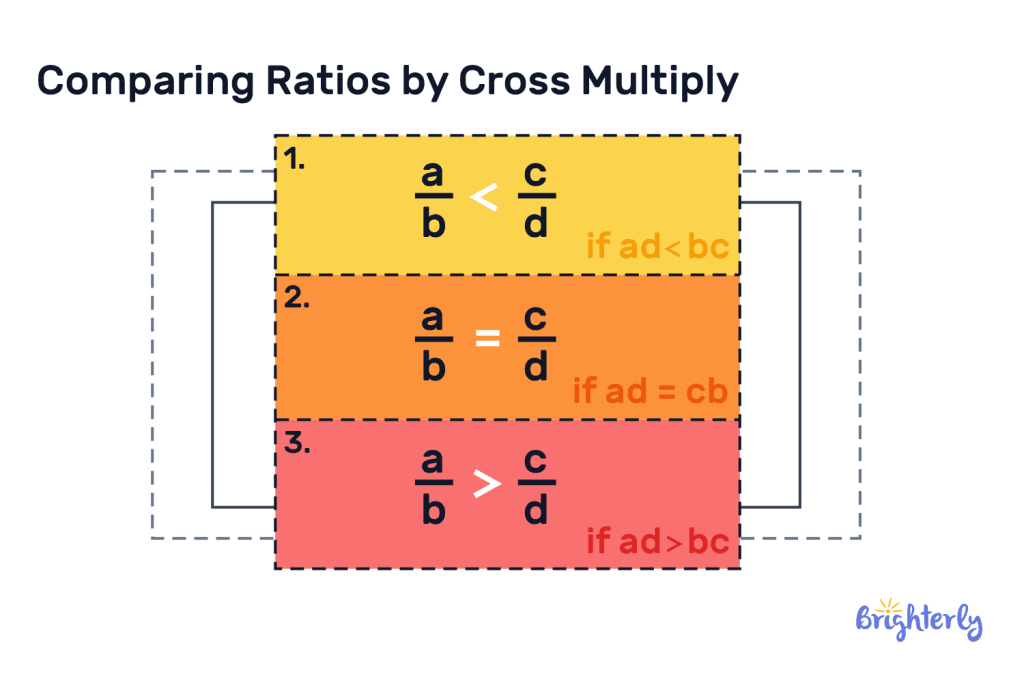
Cross multiplication to compare ratios

Did you know you can also compare ratios with cross multiplication?

Firstly, you need to convert your ratios to fractions. Let’s say we have 4:5 and 3:7. As fractions, they become ⅘ and 3/7.

Then, you would follow the same steps you take to compare unlike fractions with cross multiplication. First, multiply your numerators with your denominators:

• 4 x 7 = 28
• 5 x 3 = 15

Then, we compare our two products. 28 is larger than 15, which means the ratio of 4:5 is larger than the ratio of 3:7.

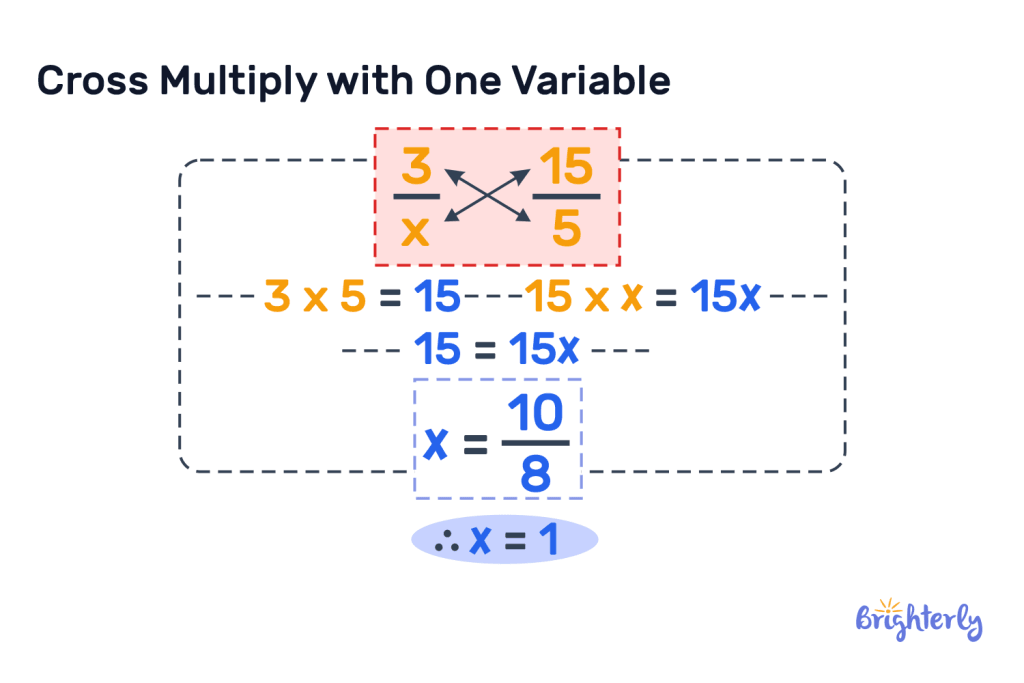
Cross multiplication with one variable

If you have a fraction with one variable, you can use cross multiplication to solve your variable.

In a fraction, a variable will be represented by a letter rather than a number, and you’ll need to perform cross multiplication to solve it.

Let’s use ⅔ and x/6 as an example. First, we cross multiply our opposing numerators and denominators.

• 2 x 6 = 12
• 3 x x = 3x

From this, you now have 12 = 3x. Then, you’ll divide both sides of the equation to solve x.

X = 12 ÷ 3 = 4.

Therefore, x = 4.

Cross multiply fractions

Cross multiplying fractions is a great way to address a lot of mathematical operations, comparisons and even solving variable numbers. Cross multiplication fractions is a key math function.

When do you cross multiply fractions?

In terms of when to cross multiply fractions, you will cross multiply fractions when:

• Comparing fractions, so you can easily see which fraction has the larger value or if they are of equal value
• Finding a variable, i.e. a missing numerator in one of your fractions
• Carrying out operations on fractions, such as addition or subtraction
• Comparing ratios by converting them to fractions and cross multiplying

How to cross multiply fractions with x?

To cross multiply fractions with x (i.e. a variable), follow these simple steps:

• Multiply the numerator of your first fraction by the denominator of your second fraction
• Multiply the denominator of your first fraction by the numerator of your second fraction
• Write the equation from your cross multiplication – this will be product 1 = product 2
• Divide both sides of your equation by your second product to find x

Solved math tasks: examples

Are you ready to try out cross multiplication yourself? Try our solved math problems and write down your answers before checking to see how many you’ve got right!

Solved math task 1

You have the ratios of 5:6 and 9:16. Compare the two ratios to determine which is larger.

Answer:

First, we multiply our opposing numerators and denominators:

• 5 x 16 = 80
• 6 x 9 = 54

Then, we compare our two products. 80 is larger than 54, so 5:6 is a larger ratio than 9:16.

Solved math task 2

We have the two fractions of ⅝ and x/4. Using cross multiplication, solve x.

Answer:

First, we multiply our opposing numerators and denominators:

• 5 x 4 = 20
• 8 x x = 8x

Then, our equation becomes 20 = 8x, and we divide both sides by 8: 20 ÷ 8 = 2.5.

Therefore, x = 2.5.

Cross multiplication: practice math problems

Cross multiplication: worksheets

Now that you know how to cross multiply fractions for different purposes, it’s time to test your knowledge! Download our fun free worksheets to become a whizz at cross multiplication.

• Ratio worksheets
• Equivalent fractions worksheets for 4th grade
• Fractions worksheets
• Simplifying fractions worksheets

Camille Ira B. Mendoza

19 articles

I am a seasoned math tutor with over seven years of experience in the field. Holding a Master’s Degree in Education, I take great joy in nurturing young math enthusiasts, regardless of their age, grade, and skill level. Beyond teaching, I am passionate about spending time with my family, reading, and watching movies. My background also includes knowledge in child psychology, which aids in delivering personalized and effective teaching strategies.