• Math tutors
• /
• Knowledge Base
• /
• Isosceles Trapezoid: Definition, Formula, and Examples

Isosceles Trapezoid: Definition, Formula, and Examples

Camille Ira B. Mendoza

reviewed by Jo-ann Caballes

Updated on October 8, 2024

Welcome to Brighterly, where we make math exciting to learn and easy to understand.

As part of our series on geometry and shapes, today we’re going to cover the isosceles trapezoid! It’s a fascinating shape that has unique properties that set it apart from other trapezoids, quadrilaterals and polygons.

Here, we’ll cover the isosceles trapezoid definition, its unique properties and how to find the area and angles of these shapes. We’ll also share examples and practice problems so you can put your knowledge to the test!

What is an isosceles trapezoid?

An isosceles trapezoid is a type of trapezoid that is defined by its lengths. It’s a key element of geometry. It is classified as both a polygon and a quadrilateral.

This four-sided closed shape has a pair of parallel sides (known as the base). It also has a pair of non-parallel sides (known as the legs) that are both the same length. The base angle pairs will add up to 180°, and all angles in the trapezoid will add up to 360°.

An isosceles trapezoid is also sometimes known as an isosceles trapezium.

Math tutors

Improve your child’s math skill today with Brighterly

Let them be at the top of their class.

Book free lesson

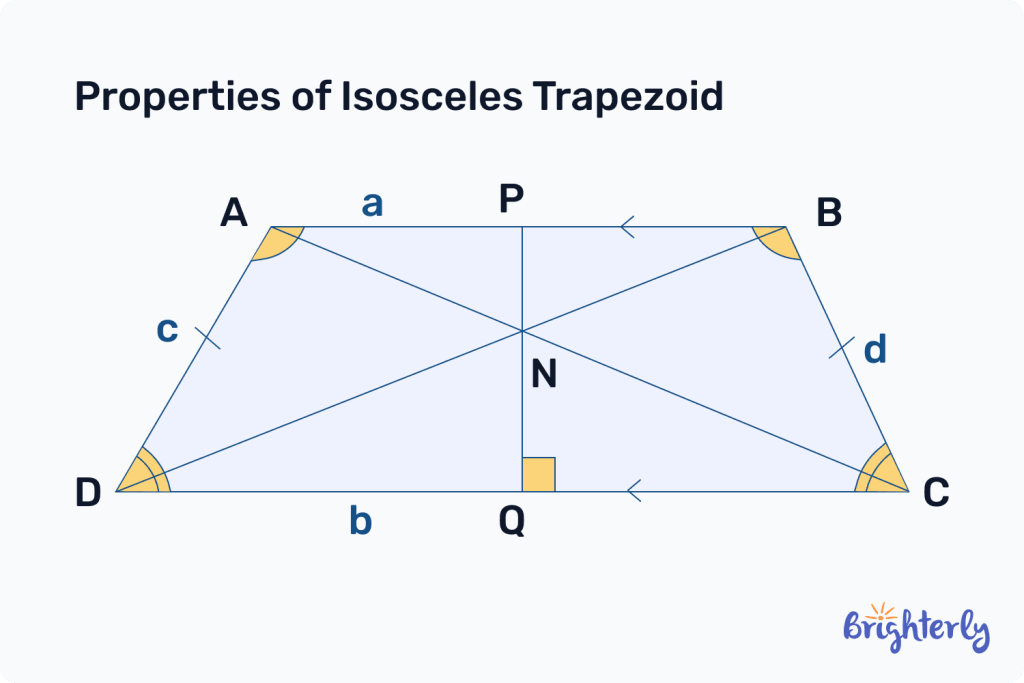
Properties of an isosceles trapezoid

The properties of an isosceles trapezoid sets it apart from other trapezoids, which are defined as a four-sided shape with one pair of parallel sides.

An isosceles trapezoid also has one pair of parallel lengths, but the main property that sets it apart is that its pair of non-parallel sides are the same length. This also means the angles at each base (the parallel sides) are equal.

Additionally, the equal lengths of the non-parallel sides means we can draw a line of symmetry at the midway points between the sides of equal length.

A fun fact about isosceles trapezoids is that they are the only trapezoids that you can inscribe into a circle!

How to find the area of an isosceles trapezoid

To find the area of an isosceles trapezoid, you’ll need to know the length of its two parallel sides and its height. Once you know these factors, you’ll be able to use a simple formula to find the area of an isosceles trapezoid.

Here’s how to find the area of an isosceles trapezoid. First, add the length of your two parallel sides together, then divide that number by 2. Once you have that number, multiply it by your isosceles trapezoid height to get its area!

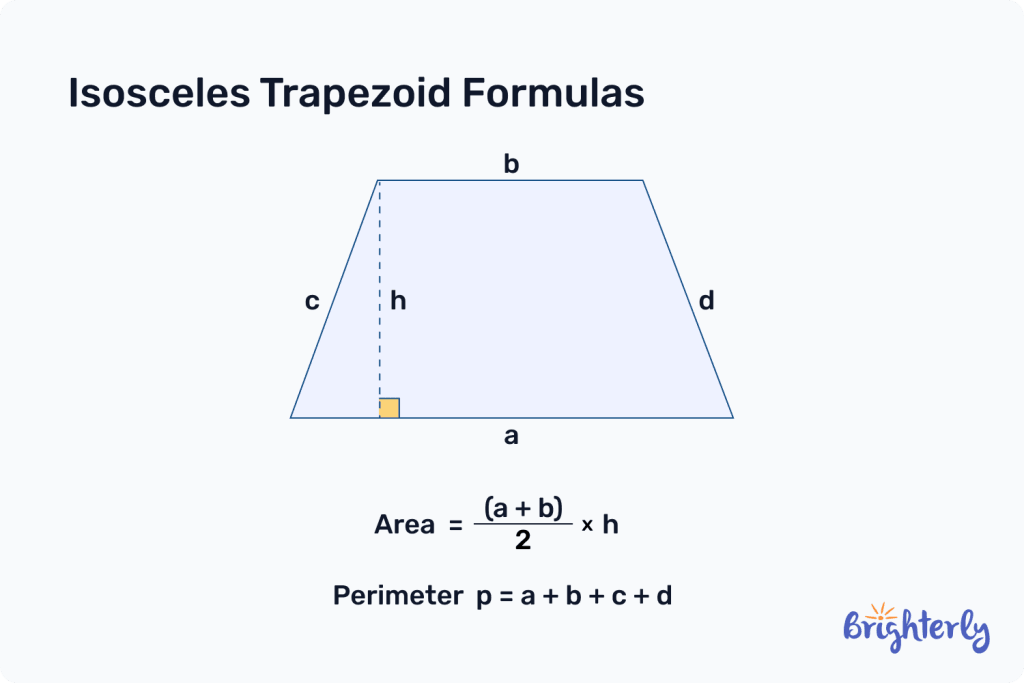
Isosceles trapezoid formula

There are two formulas that relate to isosceles trapezoids: the area and perimeter of an isosceles trapezoid.

Isosceles trapezoid area formula 

The formula to calculate the area of an isosceles trapezoid is:

Area = (sum of parallel sides ÷ 2) × height.

For example, let’s work out the area of the below isosceles trapezoid:

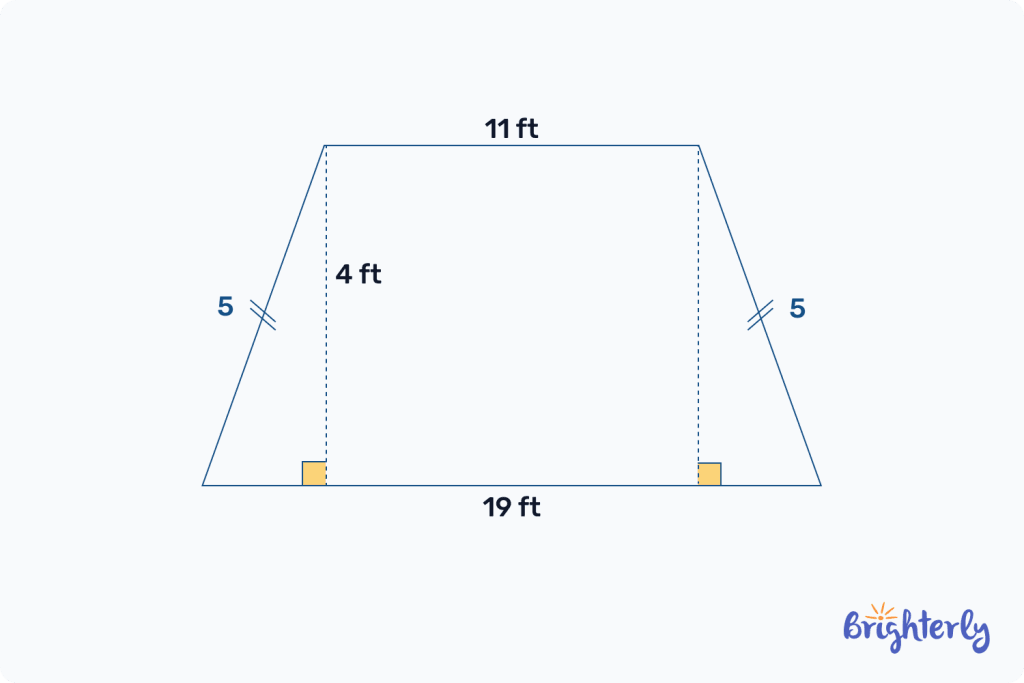
First, we add the lengths of the parallel sides together: 11 ft + 19 ft = 30 ft.

Then, we divide that by 2: 30 ft ÷ 2 = 15 ft.

Finally, multiply this number by the height. 15 x 4 = 60 ft2.

Perimeter of isosceles trapezoid formula

The formula to calculate the perimeter of an isosceles trapezoid is:

Perimeter = a + b + c + d 

Here, the letters represent the length of each side of your isosceles trapezoid.

For example, let’s work out the perimeter of the below isosceles trapezoid:

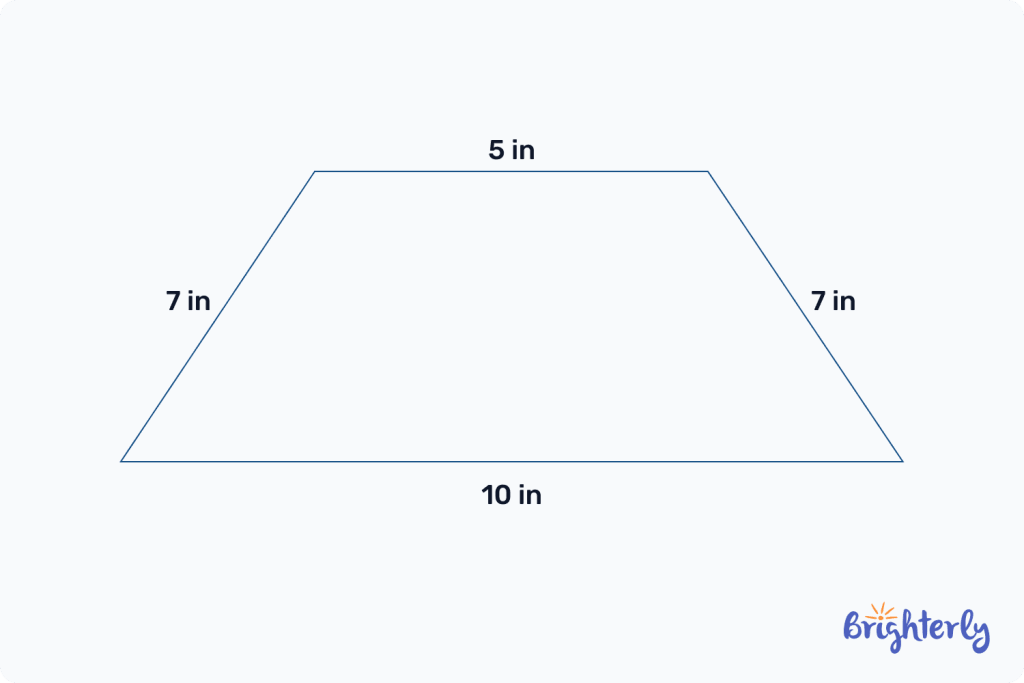
You add up all of your side lengths: 5 in + 7 in + 7 in + 10 in = 29 in.

What are the base angles of an isosceles trapezoid?

The base angles of an isosceles trapezoids, i.e. the pairs of angles on both bases, are equal to one another. This means the two smaller angles are congruent to one another, and the two larger angles are congruent to one another. The isosceles trapezoid congruent angles are on both bases, while the opposite angles are not equal.

Solved math tasks: examples

Time to test your new knowledge on isosceles trapezoids! Now that you know the isosceles trapezoid definition, try out these solved math tasks below, and then check your answers once you’ve finished to see if you’ve got them right.

Solved math task 1

You have an isosceles trapezoid with the side lengths of 5 cm, 5 cm, 6 cm and 7 cm. Work out the perimeter of the shape.

Answer:

To calculate the perimeter of an isosceles trapezoid, you add up all side lengths. 5cm + 5cm + 6cm + 7cm = 23cm.

Solved math task 2

The below figure is an isosceles trapezoid with base lengths of 6 cm and 12 cm, and a height of 4 cm. Work out its area.

Figure A:

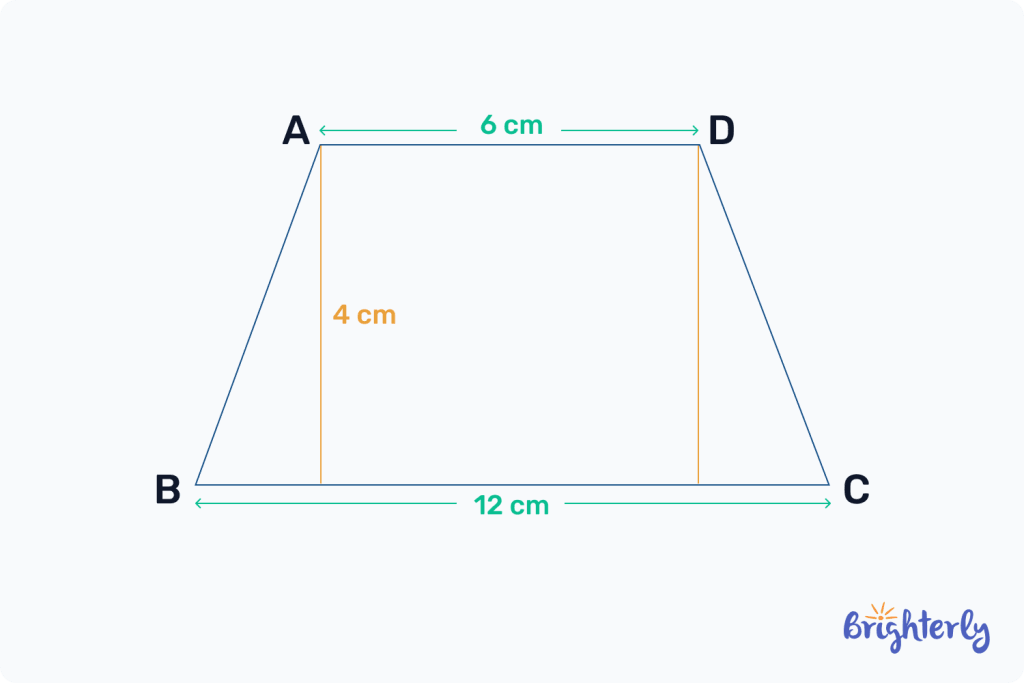
Answer:

Our first calculation will be: 

(6 cm + 12 cm ÷ 2) × 4 cm

We can further simplify it as such:

(18 cm ÷ 2 cm) x 4 cm

9 cm x 4 cm = 36 cm2

Solved math task 3

You have an isosceles trapezoid with a perimeter of 22 cm and three of the following lengths:

• 7 cm
• 3 cm
• 3 cm

What is the length of the missing side?

Answer:

Because you add all the sides of an isosceles trapezoid up to get the perimeter, to find a missing side, you just need to subtract the known sides from the perimeter.

22 cm – 7 cm – 3 cm – 3 cm = 9 cm

Isosceles trapezoids: practice math problems

Isosceles trapezoid: worksheets

Now that you know everything there is to know about the isosceles trapezoid shape, download our cool free math worksheets to practice your knowledge and become a master of this intriguing shape:

• Geometry worksheets
• Trapezoid worksheets
• Area of a trapezoid worksheets
• Area and perimeter worksheets

Camille Ira B. Mendoza

19 articles

I am a seasoned math tutor with over seven years of experience in the field. Holding a Master’s Degree in Education, I take great joy in nurturing young math enthusiasts, regardless of their age, grade, and skill level. Beyond teaching, I am passionate about spending time with my family, reading, and watching movies. My background also includes knowledge in child psychology, which aids in delivering personalized and effective teaching strategies.