Reviewed by Mary Grace Carlos
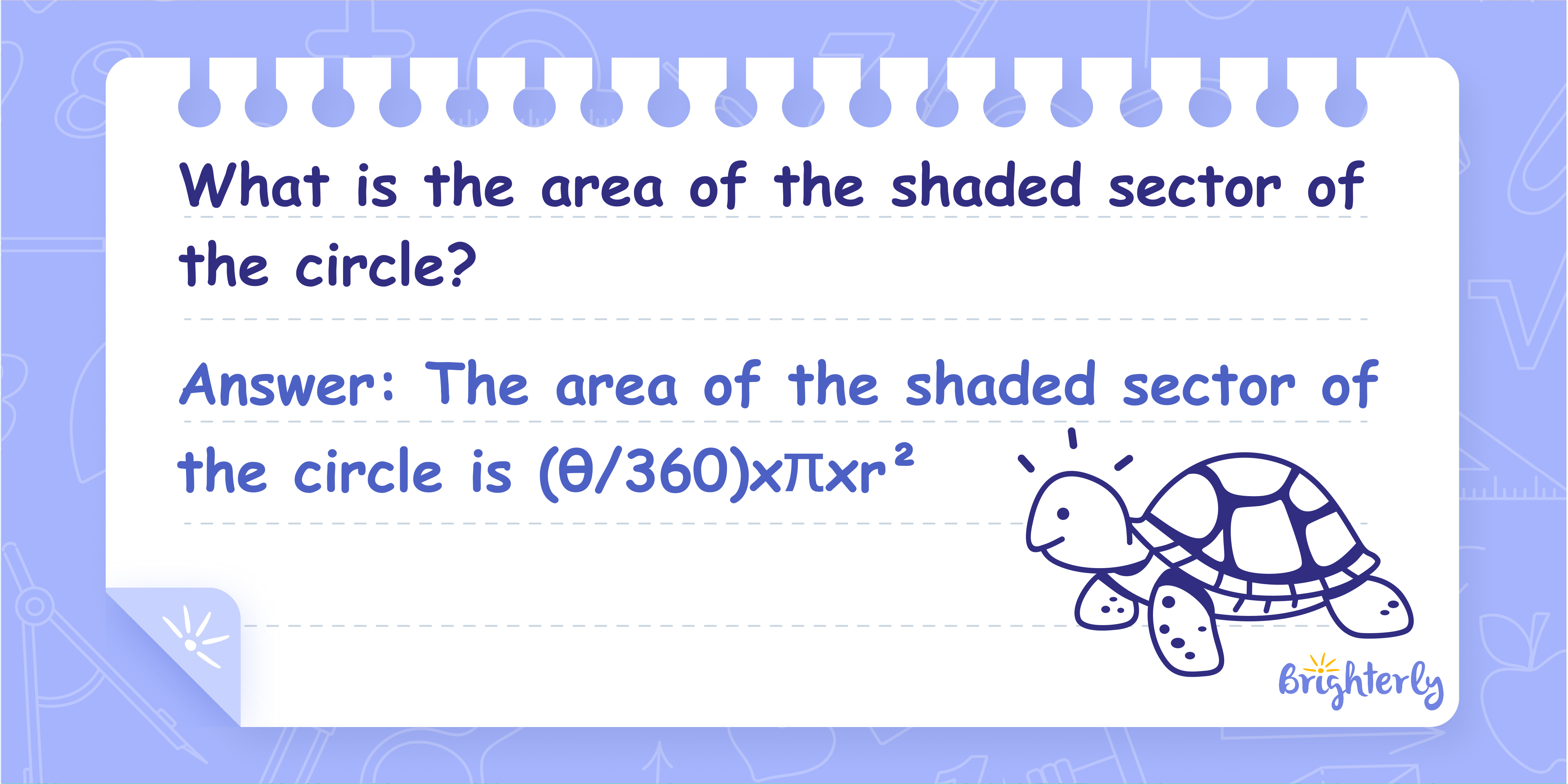
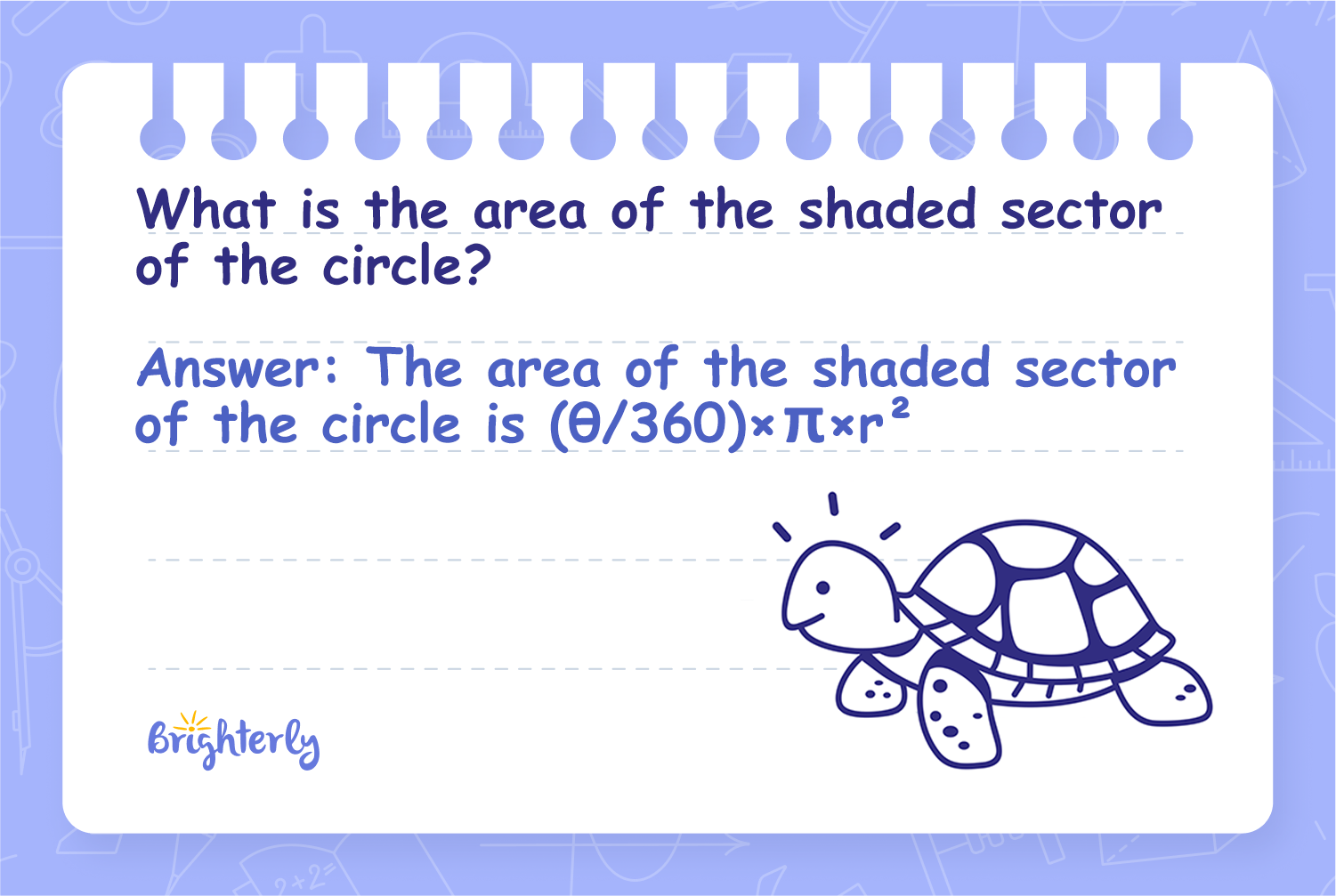
What is the area of the shaded sector of the circle?
Answer: The area of the shaded sector of the circle is (θ/360) × π × r²
The area of a sector of a circle refers to the region bounded by two radii and the arc between them. This area can be calculated when you know the circle’s radius and the central angle (θ) in degrees. Knowing how to find the area of a sector is essential for many geometry problems involving circles.
Methods
Math Tutor Explanation Using the Formula Method
The area of a shaded sector can be found directly by applying the standard sector area formula, which relates the fraction of the circle's area corresponding to the given angle.
Step 1: Step 1: Identify the central angle (θ) of the shaded sector in degrees
Step 2: Step 2: Determine the radius (r) of the circle
Math Tutor Explanation Using the Proportion Method
The proportion method involves finding what fraction of the full circle the sector represents, then multiplying this fraction by the entire area of the circle.
Step 1: Step 1: Find the fraction of the circle the sector represents by dividing the sector's angle θ by 360
Step 2: Step 2: Calculate the area of the full circle using π × r²
Step 1:
Step 2:
Math Tutor suggests: Further Practice with Circles and Sectors
Deepen your understanding of circles, sectors, and geometry with these related questions and exercises.
FAQ on Sectors of Circles
What information do I need to find the area of a sector?
You need the radius of the circle and the measure of the sector's central angle.
How do I find the length of the arc of the sector?
Arc length = (θ/360) × 2πr, where θ is the central angle in degrees and r is the radius.
What if the central angle is in radians?
Use the formula: Area = (1/2) × r² × θ, where θ is the angle in radians.
How do I find the area of the unshaded region?
Subtract the area of the shaded sector from the area of the whole circle.
Can the sector area formula be used if the radius is unknown?
You need either the radius or enough information to find it to use the standard sector area formula.
Math & reading from 1st to 9th grade
Online Summer Camp for Kids and Teens
Choose kid's grade
