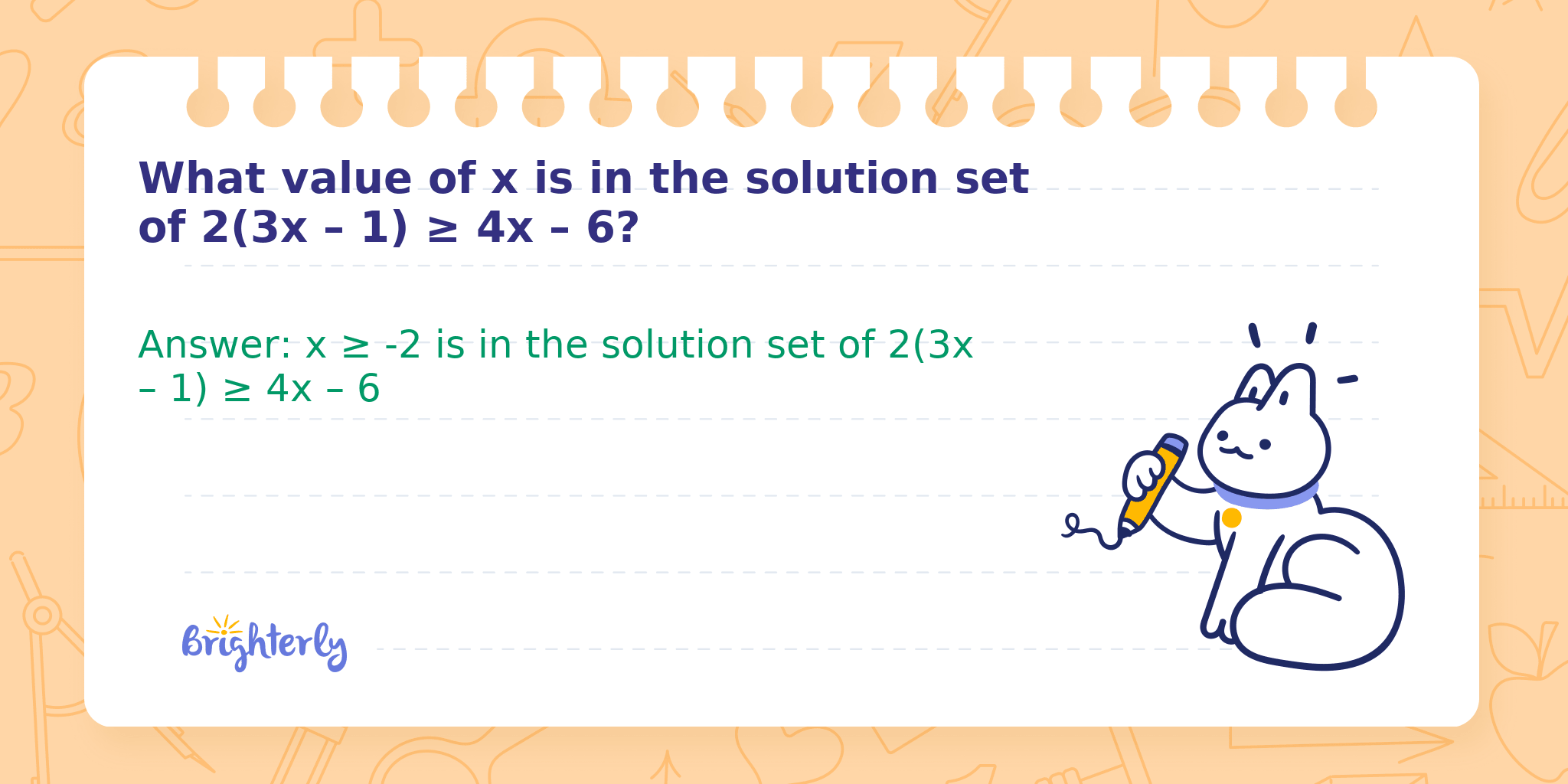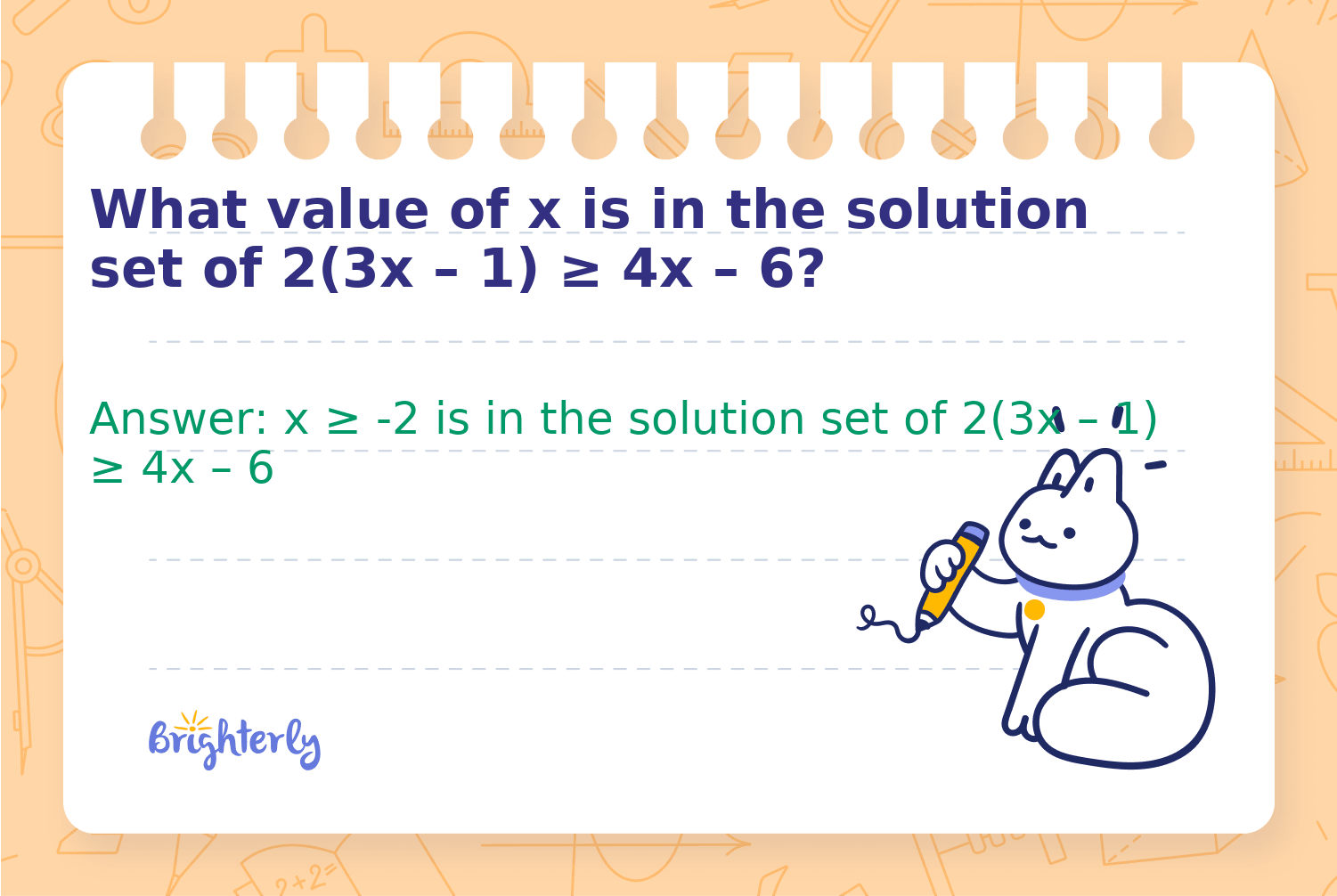Reviewed by Mary Grace Carlos
What value of x is in the solution set of 2(3x – 1) ≥ 4x – 6?
Answer: x ≥ -2 is in the solution set of 2(3x – 1) ≥ 4x – 6
This problem involves solving a linear inequality to find the set of values of x that make the inequality true. By carefully applying algebraic operations, we can isolate x and determine the correct interval for the solution set.
Methods
Math Tutor Explanation Using the Distribution and Combining Like Terms Method
Expand, rearrange, and solve the inequality step by step to isolate x.
Step 1: Step 1: Distribute the 2 on the left side so it becomes 6x – 2 ≥ 4x – 6
Step 2: Step 2: Subtract 4x from both sides to get 2x – 2 ≥ –6
Math Tutor Explanation Using Substitution and Checking Values
Pick values and check if they satisfy the inequality to verify the solution set.
Step 1: Step 1: Substitute x = –2 into the original inequality: 2(3 × –2 – 1) ≥ 4 × –2 – 6
Step 2: Step 2: Calculate both sides: 2(–6 – 1) = 2(–7) = –14; 4 × –2 – 6 = –8 – 6 = –14
Step 1:
Step 2:
Math Tutor suggests: Practice More Inequality and Equation Problems
Strengthen your understanding of solving inequalities and equations with these related exercises.
FAQ on Solving Linear Inequalities
Do you reverse the inequality sign when dividing by a negative number?
Yes, always reverse the inequality sign when you multiply or divide both sides by a negative.
Can there be more than one value in the solution set?
Yes, inequalities often have an infinite set of solutions unless the inequality is strict and there’s a unique answer.
How do you check if a value is in the solution set?
Plug the value into the original inequality and see if it results in a true statement.
What does it mean when the solution is 'x ≥ –2'?
It means all numbers greater than or equal to –2 satisfy the inequality.
Are brackets or parentheses used in interval notation for 'x ≥ –2'?
A bracket is used for –2 (inclusive), so in interval notation it is [–2, ∞).
Math & reading from 1st to 9th grade
Looking for homework support for your child?
Choose kid's grade
